Inhaltsverzeichnis
Vorverarbeitung
Die in JAG3D hinterlegten Funktion zur Vorverarbeitung sind grundsätzlich optional und müssen nicht zwingend im Vorfeld einer Ausgleichungsrechnung durchgeführt werden. So kann die Näherungskoordinatenbestimmung bereits vollautomatisch bei der Datenerhebung im Feld vorgenommen werden, wenn die Messdaten durch eine Totalstation registrierten werden. Diese Vorgehensweise ist zu empfehlen, da hierdurch direkt bei der Datenerhebung im Felde Unstimmigkeiten wie bspw. Punktverwechslungen aufgedeckt und behoben werden können. Auch eine Mittelwertbildung kann automatisiert im Feld realisiert werden, bspw. durch Satzmessprogramme, und ermöglicht eine einfache Kontrolle der erhobenen Daten.
Bestimmung von Näherungskoordinaten
Die Beschaffung geeigneter Näherungswerte ist nicht trivial, da u.a. grobe Messabweichungen in den Beobachtungsdaten vorhanden sein können. Sie ist jedoch Grundvoraussetzung für die Linearisierung der Beobachtungsgleichungen im Rahmen der Netzausgleichung. In JAG3D erfolgt die Bestimmung von Näherungswerten in einem robustifizierten, linearen Modell auf der Basis einer koordinatenbasierten Bündelblockausgleichung getrennt für Lage und Höhe. Für jeden Standpunkt werden die ggf. umgerechneten Beobachtungen in kartesische Koordinaten überführt. Hierdurch entstehen $m$ lokale Koordinatensysteme, deren jeweiliger Ursprung der $m$-te Standpunkt selbst ist. Durch eine lineare Ein-Parameter-Transformation für die Höhe bzw. eine lineare Drei-Parameter-Transformation für die Lage lassen sich jeweils zwei lokale Standpunktsysteme ineinander überführen und ggf. zusätzlich Punkte bestimmen, die innerhalb eines Systems einen Konfigurationsdefekt aufweisen z.B. durch Vorwärts-, Rückwärts- oder Bogenschnitte. Durch Mehrfachanwendung dieser Transformationsvorschrift könnten grundsätzlich alle $m$ Koordinatensysteme zu einem einheitlichen globalen Koordinatensystem zusammengefasst werden. Die sich ergebende Lösung würde jedoch sehr stark von der Reihenfolge der nacheinander ausgeführten Transformationen (Transformationsrichtung) abhängen. Aus diesem Grund wird nach den Vortransformationen eine Simultantransformation durchgeführt, bei der alle $m$ Systeme in einem geschlossenen Modell ineinander transformiert werden.
Um den Einfluss von groben Messabweichungen zu minimieren, werden die Restklaffen der Punkte analysiert. Punktbeobachtungen mit erhöhten Restklaffen werden von der Berechnung ausgeschlossen. Werden schlecht konditionierte Punkte am Ende der Berechnung protokolliert, sollten diese eingehend geprüft werden, da diese unter Umständen durch Fehlmessungen verfälscht sind. Nicht-bestimmbare Punkte oder nicht-kombinierbare Subsysteme deuten darüber hinaus auf einen Konfigurationsdefekt im Datenbestand hin und sind zu prüfen.
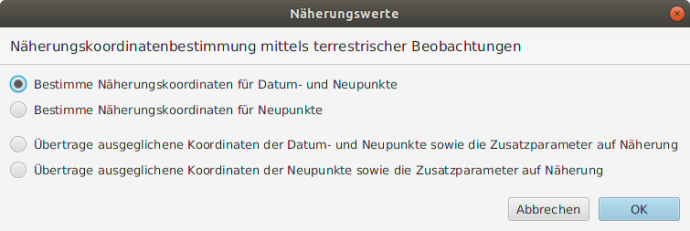
Die Näherungswertbestimmung bestimmt wahlweise die Koordinaten von Neu- und Datumspunkten bspw. in Vorbereitung auf eine freie Netzausgleichung oder nur die Neupunktkoordinaten, vgl. Abbildung 1. Stochastische Anschlußpunkte oder Festpunkte bleiben unangetastet und definieren das globale Zielsystem.
Hinweis: Da terrestrische Aufnahmen vorrangig mit Totalstationen erfolgen, liegt das Hauptaugenmerk auf der Verarbeitung vollständiger polarer Datensätze im Rahmen der Näherungswertbestimmung. GNSS-Basislinien werden derzeit nicht mit einbezogen.
| Bestimme Näherungskoordinaten für Datum- und Neupunkte | Die Koordinaten von Datum- und Neupunkten werden durch eine Bündelblockausgleichung geschätzt. Das Netzdatum wird durch das lokale Standpunktsystem definiert, welches die meisten Verknüpfungspunkte aufweist. |
|---|---|
| Bestimme Näherungskoordinaten für Neupunkte | Die Koordinaten von Neupunkten werden durch eine Bündelblockausgleichung geschätzt. Das Netzdatum ist vom Anwender vorzugeben. Dieses wird nicht validiert. |
| Übertrage ausgeglichene Koordinaten der Datum- und Neupunkte sowie die Zusatzparameter auf Näherungswerte | Die geschätzten Parameter der Datum- und Neupunkte sowie der Zusatzparameter werden als a-priori Werte übernommen. Hierdurch reduziert sich u.U. die Anzahl der notwendigen Iterationen in Folgeausgleichungen und -analysen. |
| Übertrage ausgeglichene Koordinaten der Neupunkte sowie die Zusatzparameter auf Näherungswerte | Die geschätzten Parameter der Neupunkte sowie der Zusatzparameter werden als a-priori Werte übernommen. Hierdurch reduziert sich u.U. die Anzahl der notwendigen Iterationen in Folgeausgleichungen und -analysen. |
Mittelwertbildung
Das stochastische Modell der Netzausgleichung setzt unabhängige Beobachtungen voraus. Auch wenn das Erzeugen von vollständig stochastisch unabhängigen Beobachtungen in der Praxis nahezu unmöglich ist, sollte u.a. zur Vermeidung scheinbarer Genauigkeiten (Wiederholungsgenauigkeit) versucht werden, ein möglichst stochastisch unabhängiges Beobachtungsmaterial in die Ausgleichung einzuführen. Ob eine Beobachtung (weitgehend) stochastisch unabhängig von einer anderen ist, lässt sich z.B. an der Art der Erhebung feststellen. Wurde der Messaufbau bspw. zwischen den Erhebungen nicht (wesentlich) verändert, so sind diese Beobachtungen nicht unabhängig. Als Beispiel kann hier die automatisierte Messung von mehreren Halb- oder Vollsätzen genannt werden, die i.d.R. ohne Neueinrichtung von Stand- und Zielpunkten erfolgt. Es handelt sich somit lediglich um Messungen, die unter gleichen Bedingungen wiederholt wurden, weshalb man auch von Wiederholgenauigkeit oder Präzision spricht. Abbildung 2 stellt eine aus einem Messprozess gewonnene Stichprobe dar und zeigt u.a. den Unterschied zwischen Richtigkeit, Präzision und Auflösung.
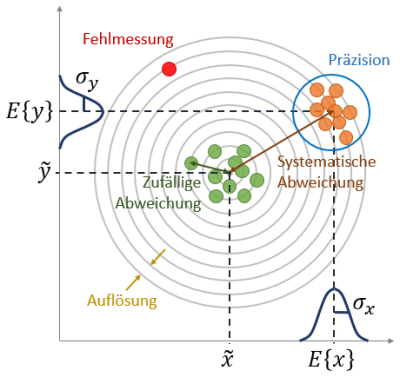
Die Präzision lässt jedoch keine Rückschlüsse auf die Richtigkeit einer Messung zu. Aus einer Streckenmessung, die bspw. 100-mal unter gleichen Bedingungen wiederholt wurde, wird man ggf. eine sehr hohe Präzision ableiten können. Wenn aber versäumt wurde, die korrekte Prismakonstante einzustellen, sind alle Strecken um den Betrag dieser fehlenden Konstante unrichtig, vgl. Abbildung 2. Wiederholungsmessungen unter gleichen Bedingungen sich daher nur bedingt geeignet, um zuverlässige a-priori Unsicherheiten abzuschätzen. Sie können jedoch verwendet werden, um grobe Fehler innerhalb einer Reihe zu detektieren oder eine statistisch zuverlässigere Größe abzuleiten, wie bspw. den Mittelwert als besten Schätzer für den Erwartungswert der Messreihe.
Aus den o.g. Gründen sollten, sofern Wiederholungsmessungen unter gleichen Bedingungen erfolgten, die Mittelwerte der jeweiligen Messreihen als Beobachtung in die Netzausgleichung eingeführt werden. Hierbei ist sicherzustellen, dass grobe Fehlmessungen zuvor ausgeschlossen wurden. JAG3D ermöglicht das gruppenweise Mitteln von gleichartigen Beobachtungen. Unter gleichartigen Beobachtungen wird verstanden, dass neben der Beobachtungsart auch die Beobachtungsrichtung sowie Instrumenten- und Tafelhöhen identisch sind:
- Eine Strecke von
AnachBwird nicht mit einer Streckenmessung vonBnachAverrechnet. - Beobachtungen, die in unterschiedlichen Gruppen vorliegen, werden nicht gemittelt.
- Deaktivierte Beobachtungen werden vom Mitteln ausgeschlossen.
- Beobachtungen, die in deaktivierten Gruppen vorliegen, werden nicht berücksichtigt.
- Beobachtungen, zu denen es im Projekt (noch) keine Punkte gibt, werden nicht gemittelt.
Es werden demnach nur die Beobachtungen gemittelt, die (theoretisch) auch bei einer Netzausgleichung herangezogen werden. Aus diesem Grund sind bereits hinreichend gute Näherungswerte notwendig, damit für die gemessenen Richtungen eine zuverlässige Zuordnung der Lage I bzw. II erfolgen kann.
Da der Mittelwert nur bei fehlerfreien Beobachtungen ein unverzerrter Schätzer ist, ist die Datenreihe vorab auf Fehlmessungen hin zu untersuchen und ggf. zu bereinigen. Hierfür eignen sich besonders robuste Schätzer, die gegenüber kontaminierten Daten resistent sind. Der Median einer Reihe ist ein solcher robuster Schätzer, der einen Bruchpunkt von $50 \%$ aufweist. Dies bedeutet, dieser Schätzer bleibt von Fehlmessungen unberührt, wenn mindestens die Hälfte der erhobenen Daten fehlerfrei ist. Der Median ist dabei ein Wert der Messreihe selbst.
$$x_{med} =\begin{cases} x_{\frac{n+1}{2}} & n \text{ ungerade}\\ x_{\frac{n}{2}} & n \text{ gerade} \end{cases}$$
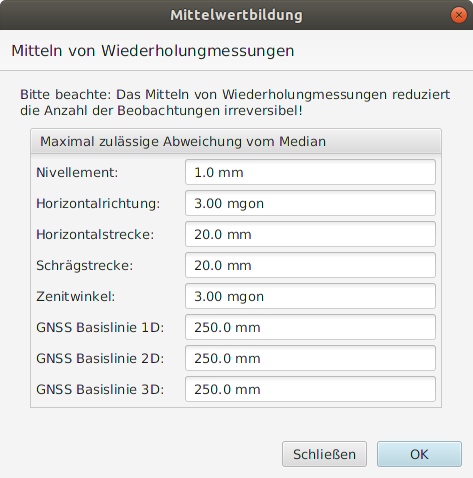
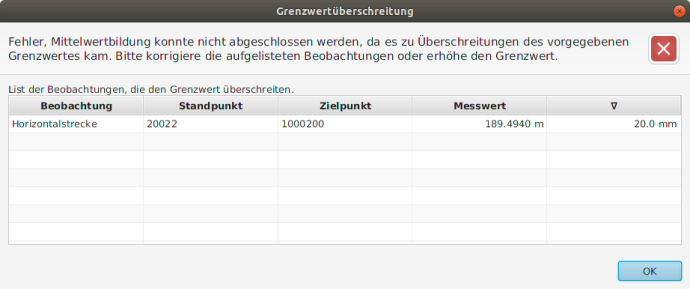
Während der Berechnung wird der Median der Reihe gebildet. Die Abweichungen der einzelnen Beobachtungen vom Median werden ermittelt und mit dem vorgegebenen Grenzwert verglichen, vgl. Abbildung 3. Nur wenn der Grenzwert bei keiner Beobachtung überschritten wird, werden die gemittelten Daten in der Datenbank gespeichert. Überschreiten Beobachtungen hingegen den vorgegebenen Grenzwert, erfolgt keine Mittelwertbildung. Die Grenzwertüberschreitungen werden protokolliert und zur weiteren Analyse ausgegeben, vgl. Abbildung 4.
Hinweis: Die Mittelwertbildung führt stets zu einer Datenreduktion. Der Berechnungsprozess kann nicht rückgängig gemacht werden, sodass es empfehlenswert ist, vor der Mittelwertbildung eine Kopie vom aktuellen Auswerteprojekt zu erzeugen.