Inhaltsverzeichnis
Zuverlässigkeitsmaße in der Netzausgleichung
Nach einer erfolgreichen Ausgleichung sind neben den Koordinaten und ggf. Zusatzunbekannten auch die Qualität der erzielten Ergebnisse bzgl. der inneren und äußeren Zuverlässigkeit zu bewerten. Hierzu zählen das Aufdecken von Modellstörungen, die gegenseitige Kontrollierbarkeit von Beobachtungen oder das Abschätzen des Einflusses einer unentdeckten Modellstörung auf die ausgeglichenen Parameter. Alle Analysemethoden setzen voraus, dass das Netz eine hinreichend große Überbestimmung besitzt und sich die einzelnen Beobachtungen ausreichend untereinander kontrollieren.
Genauigkeitsmaße der Parameter
Die Genauigkeitsmaße der geschätzten Parameter z.B. die Koordinaten der Netzpunkte werden nach der Ausgleichungsrechnung aus der Varianz-Kovarianz-Matrix der Parameter abgeleitet. Diese ergibt sich aus der Kofaktormatrix $\mathbf{Q_{\hat x \hat x}}$, die entweder mit dem a-priori Varianzfaktor $\sigma^2_0$
$$\mathbf{C_{\hat x \hat x}}=\sigma_0^2\mathbf{Q_{\hat x \hat x}}$$
oder dem aus der Stichprobe abgeleiteten empirischen a-posteriori Varianzfaktor $\hat{\sigma}_0^2$ skaliert wurde.
$$\mathbf{\hat{C}_{\hat x \hat x}}=\hat{\sigma}_0^2\mathbf{Q_{\hat x \hat x}}$$
Die Wahl des zu berücksichtigenden Varianzfaktors sollte problemspezifisch erfolgen. Insbesondere bei sehr kleinen Stichproben ist der a-priori Varianzfaktor häufig repräsentativer als der empirisch bestimmte a-posteriori Varianzfaktor.
Während auf der Hauptdiagonalen die Varianzen der Parameter angeordnet sind, befinden sich auf den Nebendiagonalen die Kovarianzen, welche die (linearen) Abhängigkeiten zwischen den Parametern quantifiziert und häufig durch den Korrelationskoeffizient ausgedrückt wird. Der Korrelationskoeffizient lautet für das $i$-te und $j$-te Element aus $\mathbf{Q_{\hat x \hat x}}$
$$\rho = \frac{q_{ij}}{\sqrt{q_{ii} \cdot q_{jj}}}$$
Während für $\rho \gt 0$ eine positive Korrelation besteht, d.h. tendenziell fallen bzw. steigen beide Parameter gemeinsam, sind die Parameter für $\rho \lt 0$ negativ korreliert, d.h. tendenziell steigt einer der beiden Parameter an während der andere abfällt. Für $\rho = 0$ sind die Parameter vollständig (linear) unabhängig, d.h. die Änderung eines Parameters wirkt sich nicht auf den anderen aus.
Die geschätzten Standardunsicherheiten $\sigma$ der Parameter z.B. der ausgeglichenen Koordinaten eines Punktes können demnach direkt aus der Varianz-Kovarianz-Matrix abgelesen werden. Zu beachten ist, dass die Varianz-Kovarianz-Matrix datumsabhängig ist. Dies bedeutet, dass bspw. die Standardunsicherheiten $\sigma$ nicht invariant gegenüber Netzverdrehungen sind und sich daher nur bedingt zur Genauigkeitsbeurteilung eignen. Ein punktbezogenes rotationsinvariantes Genauigkeitsmaß sind hingegen die Halbachsen der Konfidenzbereiche.
Durch spektrale Zerlegung der punktbezogenen Sub-Kofaktormatrix $\mathbf{Q_{\hat x \hat x}}_{ii}$ werden die Halbachsen und die Orientierung des $n$-dimensionalen Hyperellipsoids gewonnen. Während sich für $n=3$ ein Ellipsoid ergibt, erhält man für $n = 2$ eine Ellipse und für $n = 1$ ein einfaches Intervall. Die Halbachsen bilden somit die Extremstellen des Konfidenzbereichs.
$$\mathbf{Q_{\hat x \hat x}}= \mathbf{\begin{bmatrix} \mathbf{Q_{\hat x \hat x}}_{ii} & \mathbf{Q_{\hat x \hat x}}_{ij} & \dots\\ \mathbf{Q_{\hat x \hat x}}_{ji} & \mathbf{Q_{\hat x \hat x}}_{jj} & \dots\\ \vdots & \vdots & \ddots \end{bmatrix}}$$
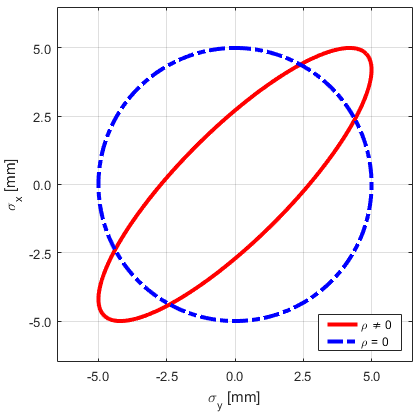
Abbildung 1 stellt für zwei Punkte die zugehörigen (einfachen) Konfidenzellipsen (Standardellipse nach Helmert; früher häufig auch Fehlerellipse) gegenüber. Während die Standardunsicherheiten $\sigma_x = \sigma_y = 5~\rm{mm}$ bei beiden Punkten identisch sind, lässt sich aus der Form der Ellipsen erkennen, dass der Konfidenzbereich der roten Ellipse kleiner ist als der der blauen. Beide Punkte weisen somit nicht dieselbe Unsicherheit auf. Die Koordinatenachsen-bezogenen Standardunsicherheiten sind demnach nur aussagekräftig, wenn diese mit den Halbachsen des Konfidenzbereichs (näherungsweise) zusammenfallen, siehe blaue Ellipse. Die Forderung nach homogenen und isotropen Konfidenzbereichen bedeutet, dass im 2D-Fall die Ellipse zu einem Kreis und im 3D-Fall das Ellipsoid zu einer Kugel entartet.
Im Folgenden soll explizit nur der räumliche Fall skizziert werden. Für $n \lt 3$ vereinfacht sich die Darstellung sinngemäß. Die $i$-te punktbezogene Sub-Kofaktormatrix $\mathbf{Q_{\hat x \hat x}}_{ii}$ lautet
$$\mathbf{Q_{\hat x \hat x}}_{ii}= \begin{pmatrix} q_{xx}&q_{xy}&q_{xz}\\ q_{xy}&q_{yy}&q_{yz}\\ q_{xz}&q_{yz}&q_{zz}\\ \end{pmatrix}_{ii}$$
Die drei Halbachsen $a$, $b$ und $c$ ergeben sich aus den (sortierten) Eigenwerten $\mathbf{\lambda} = [\lambda_{max}, \lambda_{mid}, \lambda_{min}]^T$ und dem gewählten Varianzfaktor. Für den a-priori Varianzfaktor $\sigma_0^2$ gilt
$a = \sigma_0 \sqrt{ \lambda_{max} }$, $b = \sigma_0 \sqrt{ \lambda_{mid} }$, $c = \sigma_0 \sqrt{ \lambda_{min} }$
und für den a-posteriori Varianzfaktor $\hat{\sigma}_0^2$ entsprechend
$\hat{a} = \hat{\sigma}_0 \sqrt{ \lambda_{max} }$, $\hat{b} = \hat{\sigma}_0 \sqrt{ \lambda_{mid} }$, $\hat{c} = \hat{\sigma}_0 \sqrt{ \lambda_{min} }$
Die Orientierung lässt sich aus den drei korrespondierenden Eigenvektoren $\mathbf{m}$ ableiten.
$$\mathbf{M}=\left [\begin{matrix} \mathbf{m}_{max}&\mathbf{m}_{mid}&\mathbf{m}_{min} \end{matrix} \right ]$$
worin die Modalmatrix $\mathbf{M}$ eine orthogonale Matrix mit $\det \mathbf{M} = +1$ ist, die sich in drei Einzelrotationen mit den Eulerwinkeln $\alpha$, $\beta$ und $\gamma$ zerlegen lässt.
$$\mathbf{M}=\mathbf{R_x}(\alpha)\mathbf{R_y}(\beta)\mathbf{R_z}(\gamma)$$
Die folgende Tabelle zeigt die maximale Sicherheitswahrscheinlichkeit unter Berücksichtigung von $\sigma_0$ in Abhängigkeit der Dimension $n$ für die so gebildeten einfachen Konfidenzbereiche.
| n | Wahrscheinlichkeit |
|---|---|
| 1 | 68,27 % |
| 2 | 39,35 % |
| 3 | 19,87 % |
Aufgrund der geringen Sicherheitswahrscheinlichkeit des einfachen Konfidenzbereichs von 40 % bzw. 20 % für einen Lage- bzw. Raumpunkt, werden die Halbachsen i.d.R. unter der Annahme der Normalverteilung mit einem Quantil der Fisher-Verteilung skaliert, sodass sich ein vergrößerter Konfidenzbereich mit einer entsprechend höheren Sicherheitswahrscheinlichkeit ergibt. In JAG3D wird die Sicherheitswahrscheinlichkeit bzw. das Konfidenzniveau $\left(1 - \alpha\right)$ vom Anwender vorgegeben. Die Längen der Halbachsen des Konfidenzbereichs hängen somit von der Sicherheitswahrscheinlichkeit und vom gewählten Varianzfaktor ab. Für a-priori Varianzfaktor-bezogene Konfidenzbereiche gilt für die Halbachsen
$$\sqrt{\sigma_0^2 \cdot \lambda \cdot n \cdot F_{n,\infty}}$$
Entsprechend gilt für die Halbachsen von Konfidenzbereichen, die sich auf den empirisch ermittelten a-posteriori Varianzfaktor beziehen
$$\sqrt{\hat{\sigma}_0^2 \cdot \lambda \cdot n \cdot F_{n,r}}$$
worin $r$ der Gesamtfreiheitsgrad der Ausgleichung ist.
Redundanzanteil
Ein Maß für die Kontrollierbarkeit von unkorrelierten Beobachtungen liefert die Redundanzmatrix $\mathbf{R}$
$$\mathbf{R} = \mathbf{Q_{vv}P}$$
worin $\mathbf{P}$ die (diagonale) Gewichtsmatrix des stochastischen Modells und $\mathbf{Q_{vv}}$ die Kofaktormatrix der Beobachtungsresiduen sind. Auf der Hauptdiagonalen von $\mathbf{R}$ stehen die sogenannten Redundanzanteile $r_i$ für jede Beobachtung. Für stochastisch unabhängige Beobachtungen stellt der Redundanzanteil $r_i$ einer Beobachtung ein normiertes Zuverlässigkeitsmaß dar und zeigt an, wie gut die betreffende Beobachtung durch die übrigen Beobachtungen kontrolliert wird. Während ein Redundanzanteil von $r_i = 0$ bedeutet, dass die Beobachtung nicht kontrolliert ist, repräsentiert $r_i = 1$ eine vollständige Kontrolle. Gelegentlich wird $r_i$ in Prozent angeben und durch den Parameter $EV_i [\%] = 100 \cdot r_i$ ausgedrückt. Als Faustregel für den Redundanzanteile $r_i$ gilt:
- $0.0 \leq r_i \lt 0.1$ → schlecht kontrollierbar,
- $0.1 \leq r_i \lt 0.3$ → ausreichend kontrollierbar,
- $0.3 \leq r_i \lt 0.7$ → gut kontrollierbar,
- $0.7 \leq r_i \leq 1.0$ → sehr gut kontrollierbar.
Hinweis: Es lässt sich leicht zeigen, dass selbst ein Redundanzanteil von $r_i > 0.999$ nicht ausreichen muss, um eine Modellstörung in der betreffenden Beobachtung eindeutig zu identifizieren. Redundanzanteile sind schematisch sondern stets im Kontext des Ausgleichungsproblems zu bewerten.
Die Summe aller $r_i$ bzw. die Spur der Matrix $\mathbf{R}$ liefert den Gesamtfreiheitsgrad $r = \tr(\mathbf{R})$ der Ausgleichung. Die Kontrollierbarkeit einer Beobachtung steigt i.A., wenn die Anzahl an Beobachtungen $n$ erhöht wird. Dieser Forderung stehen jedoch vor allem wirtschaftliche Aspekte gegenüber. Mithilfe des Redundanzanteils $r_i$ lässt sich durch $1 - r_i$ der Grad der Überschüssigkeit angeben. Hierdurch lässt sich bemessen, welchen Anteil die Beobachtung am Ausgleichungsergebnis mit einbringt.
Modellstörung
Unter einer Modellstörung $\mathbf{\nabla}$ verstehen wir grundsätzlich einen Fehler im funktionalen Modell oder/und stochastischen Modell der Ausgleichung. Eine angezeigte Diskrepanz kann demnach durch das Fehlen eines Zusatzparameters wie bspw. einen Maßstab bei einer Streckengruppe hervorgerufen werden. Gleichzeitig kann aber auch eine zu optimistisch gewählte a-priori Unsicherheit für das Anschlagen des statistischen Test verantwortlich sein. Eine Trennung zwischen beiden Ursachen ist daher nur bedingt möglich.
Die Größe einer möglichen Modellstörung $\mathbf{\nabla}$ wird formal durch das Erweitern des Parametervektors $\mathbf{x}$ und einer Modifikation im funktionalen Modell durch die Designmatrix $\mathbf{B}$ ermittelt. In dem erweiterten Ausgleichungsmodell werden demnach $j$ Zusatzparameter $\mathbf{\nabla}$ mitgeschätzt.
$$\mathbf{l} + \mathbf{v} = \mathbf{A}\mathbf{\hat{x}} + \mathbf{B}\mathbf{\nabla}$$
Das Schätzen der Zusatzparameter $\mathbf{\nabla}$ und der zugehörigen Kofaktormatix $\mathbf{Q_{\nabla\nabla}}$ erfordert keine Neuausgleichung und kann direkt aus den Resultaten des nicht-erweiterten Modells abgeleitet werden. Der Lösungsvektor $\mathbf{\nabla}$ ergibt sich aus
$$\nabla = -\mathbf{Q_{\nabla\nabla}}\mathbf{B}^T\mathbf{Pv}$$
worin $\mathbf{P}$ die Gewichtsmatrix des stochastischen Modells, $\mathbf{v}$ die Residuen der Beobachtungen und $\mathbf{Q_{\nabla\nabla}}$ die zu $\mathbf{\nabla}$ korrespondierende Kofaktormatix darstellt.
$$\mathbf{Q_{\nabla\nabla}} = (\mathbf{B}^T\mathbf{PQ_{vv}PB})^{-1} = (\mathbf{B}^T\mathbf{PRB})^{-1}$$
Da eine rechen- und zeitintensive Neuausgleichung entfallen kann, lassen sich mit vertretbarem Aufwand verschiedene Störmodelle analysieren und die geschätzten Modellstörungen $\mathbf{\nabla}_i$ in Relation zur Genauigkeit statistisch bewerten. JAG3D führt für jede Beobachtung ein spezifisches Störmodell ein. Eine signifikante Modellstörung liegt vor, wenn die Nullhypothese $\rm{E}\{\mathbf{\nabla}_i\} =\mathbf{0}|H_0$ verworfen werden muss.
Offensichtlich können nur Beobachtungen geprüft werden, deren Redundanzanteil $r_i \gt 0$ ist, da zur Bestimmung von $\mathbf{\nabla}_i$ bzw. $\mathbf{Q_{\nabla\nabla}}_i$ die Redundanzmatrix $\mathbf{R}$ notwendig ist. Beobachtungsbezogene Störmodelle können demnach nur berechnet werden, wenn die Beobachtung durch die übrigen Beobachtungen im Netz kontrolliert wird.
Einfluss auf die Punktlage
Um Abzuschätzen, welchen Einfluss eine geschätzte Modellstörung $\mathbf{\nabla}_i$ auf die berührenden Punkte der korrespondierenden Beobachtung ausübt, ist der Einfluss auf die relative Punktlage $\mathbf{EP}_i$ zur analysieren.
$$\mathbf{EP}_i=\mathbf{A}_{\mathbf{x},i}\nabla\mathbf{x}_i$$
worin $\mathbf{A}_{\mathbf{x},i}$ den koordinatenbezogenen Anteil der Designmatrix $\mathbf{A}$ des funktionalen Modells, $\nabla\mathbf{x}_i$ die Auswirkung einer Modellstörung $\nabla_i$ auf die geschätzten Koordinaten beschreiben
$$\nabla\mathbf{x}_i=\mathbf{Q_{\hat{x}\hat{x}}}{\mathbf{\bar{A}_{x}}}^T{\mathbf{PB}}_i {\mathbf{\nabla}}_i$$
und
$$\mathbf{\bar{A}_{x}}=\mathbf{A_x} - \mathbf{A_z}(\mathbf{A_z}^T\mathbf{PA_z})^{-1}\mathbf{A_z}^T\mathbf{PA_x}$$
die um den Anteil der Zusatzunbekannten $\mathbf{A_z}$ reduzierte Designmatrix $\mathbf{A}$ sind. Enthält das funktionale Modell für die betreffende Beobachtung keine Zusatzparameter, so ergibt sich $\mathbf{EP}_i$ direkt aus
$$\mathbf{EP}_i = (\mathbf{E} - \mathbf{R}_i)\mathbf{B}_i\nabla_i$$
wodurch noch einmal die Wichtigkeit eines redundanten Netzes unterstrichen wird. Die Auswirkungen einer geschätzten Modellstörung auf die relative Punktlage hängt somit direkt vom Grad der Überschüssigkeit $1 - r_i$ ab. Bei einem Redundanzanteil von $r_i = 0.9$ würden demnach nur 10 % der geschätzten Modellstörung $\nabla_i$ einen Einfluss auf die relative Punktlage der berührenden Punkte ausüben.
Der Einfluss auf die relative Punktlage $\mathbf{EP}$ sollte somit auch bei der Entscheidung, ob eine Beobachtung im Datenbestand verbleibt, berücksichtigt werden. Grenzwerte werden u.a. bei hoheitlichen Aufgaben von den Landesvermessungsbehörden festgesetzt. Für Liegenschaftsvermessungen in Baden-Württemberg1) ist ein Grenzwert von 3 cm vorgesehen. Für Richtungsbeobachtungen oder Zenitwinkel ist $EP$ daher noch in eine Querabweichung umzurechnen.
Einflussbemessung der Netzverzerrung
Die ungünstigste Auswirkung einer nicht-erkannten Modellstörung auf die ausgeglichenen Koordinaten kann durch die skalare Größe $EF$ beschrieben werden. Diese Maßzahl wird häufig als Netzverzerrung oder auch Einflussfaktor ($EF$) bezeichnet.
$$EF^2=\frac{1}{\sigma^2_0}\nabla\mathbf{x}^T\mathbf{Q_{\hat{x}\hat{x}}^{-1}}\nabla\mathbf{x}$$
Die maximale Verfälschung ergibt sich aus
$$EF \cdot SP = EF \cdot \sigma_{P,max}$$
worin $\sigma_{P,max}$ die maximale mittlere Unsicherheit der $k$ Koordinaten im Netz ist und sich aus
$$\sigma^2_{P,\max} = \max(\tr \mathbf{Q}_{\mathbf{\hat x \hat x}_i}, i=1, 2 ,..., k)$$
ergibt. Jäger et al. (2005) führen an, dass diese Einflussbemessung grundsätzlich überschätzt wird. Dennoch findet sich diese Kenngröße in den Verwaltungsvorschriften der Länder und ist bei der Netzbeurteilung mit zu berücksichtigen. In Baden-Württemberg2) ist ein Grenzwert von 15 cm für Liegenschaftsvermessungen noch zulässig.
