Inhaltsverzeichnis
Analyse
JAG3D bietet eine Reihe von Werkzeugen, mit denen die erhobenen Daten nach der Ausgleichung schneller analysiert werden können. Alle bereitgestellten Funktionen sind über den Hauptmenüpunkt Analyse zu erreichen.
Punktkongruenz
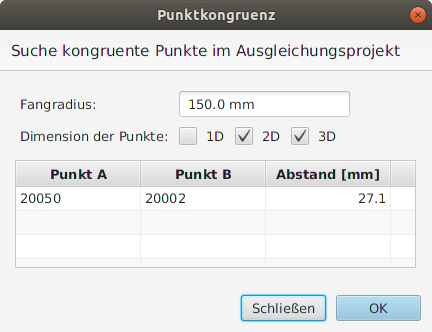
Gerade bei großen Netzen, bei denen die Aufnahme an mehreren Messtagen stattfand oder von unterschiedlichen Sachbearbeitern durchgeführt wurde, kann es zu uneinheitlich vergebenen Punktnamen für identische Punkte kommen. Um diese doppelten Punkte aufzudecken, kann diese Analysefunktion zum Aufsuchen von kongruenten Punkten in JAG3D genutzt werden.
Die euklidische Norm zwischen allen Punkten im Ausgleichungsprojekt wird hierzu ermittelt und mit dem vorgegebenen Grenzwert verglichen. Unterschreitet die Norm den Grenzwert, wird das Punktpaar in der Tabelle ausgegeben, vgl. Abbildung 1. Die Suche nach kongruenten Punkten kann auf die gewünschten Punktdimensionen beschränkt werden.
| Fangradius | Der Fangradius definiert den Grenzwert zur Bewertung der ermittelten euklidischen Norm. Bei Unterschreitung der Norm werden die betroffenen Punkte als kongruent in der Ergebnistabelle ausgewiesen. |
|---|---|
| Dimension der Punkte | Die Suche nach kongruenten Punktpaaren kann bzgl. der Punktdimension eingeschränkt werden. Dies ist insbesondere in kombinierten, hybriden Netzen mit unterschiedlichen Punktdimensionen zu empfehlen, da bspw. im unbewegten Gelände Höhenpunkte häufig nur geringe Variationen aufweisen und es hierdurch zu Fehlentscheidungen kommen kann. |
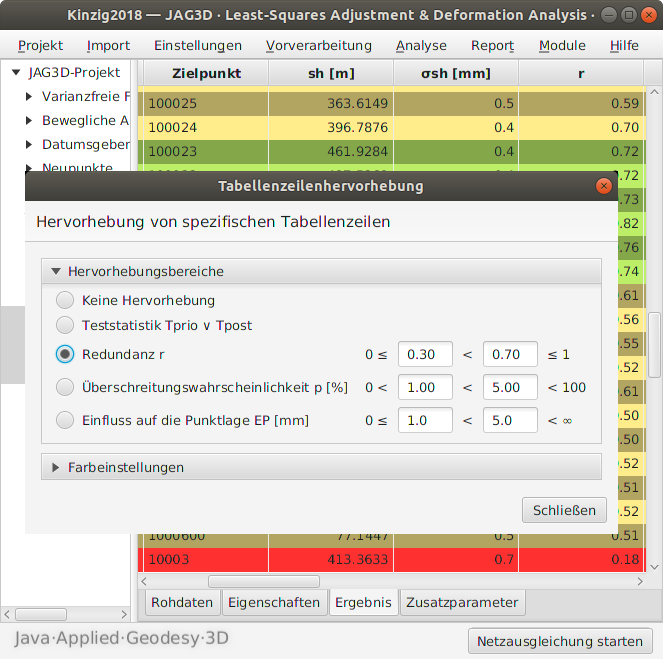
Zeilenhervorhebung
Das Hervorheben von bestimmten Tabellenzeilen (Tabellenschema) dient zum schnellen Auffinden von Schwachstellen im Datenbestand. Hierzu werden die Datensätze in den Datentabellen nach benutzerspezifischen Vorgaben, vgl. Abbildung 2, im Dreifarbenprinzip (z.B. Ampelfarben: rot, gelb, grün) eingefärbt. Das Farbschema kann nutzerspezifisch gewählt werden. Hierbei beschreibt die erste Farbe das Optimum. Das Kriterium wird vollumfänglich eingehalten. Die Defaultfarbe ist grün. Die zweite Farbe kennzeichnet den Bereich, der noch als akzeptabel angesehen wird für das gewählte Kriterium. Die Defaultfarbe ist gelb. Liegt der Wert hingegen außerhalb des zulässigen Bereichs, so wird die zugehörige Tabellenzeile mit der dritten Farbe eingefärbt. Die Defaultfarbe ist rot. Einige Kriterien sind boolesch, sodass diese nur über zwei Farbabstufungen darstellbar sind.
| Keine Hervorhebung | Die Tabellen werden in der Defaultdarstellung von JavaFX dargestellt. Eine Hervorhebung findet nicht statt. |
|---|---|
| Teststatistik $Tprio ∨ Tpost$ | In Abhängigkeit der Testentscheidung eines Hypothesentests werden die Tabellenzeilen boolesch hervorgehoben. |
| Redundanz $r$ | Das Maß für die Kontrollierbarkeit einer Beobachtung ist der Redundanzanteil $r$. Hierbei handelt es sich bei unkorrelierten Beobachtungen um ein normiertes Maß im Intervall zwischen $0-1$, welches gelegentlich auch in prozentualer Form zwischen $0-100 \%$ angegeben wird. Durch das Festlegen eines mittleren Intervalls werden die Datensätze eingefärbt. |
| Überschreitungswahrscheinlichkeit $p$ | Durch das Festlegen eines kritischen Wertes (durch Definition der Irrtumswahrscheinlichkeit und der Macht des Tests) liegt der Grenzwert zum Bewerten einer Hypothese fest. Je dichter die berechnete Teststatistik am vorgegebenen kritischen Wert (Quantil) liegt, desto abhängiger ist die Testentscheidung von den (willkürlich) gewählten Einstellungen. Wünschenswert wäre, dass die Testentscheidung auch bei (leicht) variierenden Einstellungen invariant bleibt. Diese Vorgehensweise findet sich auch in einigen vermessungstechnischen Vorschriften wieder, wenn die Beurteilung der normierten Verbesserung $NV$ in Klassenbreiten erfolgt. Üblich sind folgende Intervalle: $NV \lt 2,0$ Kein grober Fehler erkennbar, $2,0 \leq NV \lt 3,0$ Grober Fehler möglich und $3,0 \leq NV$ Grober Fehler sehr wahrscheinlich. Diese Formulierung beschränkt sich jedoch auf terrestrische Beobachtungen und ist daher nicht allgemein. Die Teststatistik einer GNSS-Basislinie könnte mit diesem einfachen Ansatz nicht klassifiziert werden, da die normierte Verbesserung nur für eindimensionale Modellstörungen anwendbar ist. Aus diesem Grund ist ein allgemein gültiger Ansatz für die Zeilenhervorhebung gewählt worden, der auf der Wahrscheinlichkeit für den Fehler 1. Art beruht und in den Ergebnistabellen mit $\log{p}$ bezeichnet wird. Statt der Definition der Intervallgrenzen durch kritische Werte wird hier die gewünschte Wahrscheinlichkeit $p$ zur Bewertung herangezogen. |
| Einfluss auf die Punktlage $EP$ | Der Einfluss auf die relative Punktlage $EP$ gibt an, in wie weit sich eine geschätzte Modellstörung auf die Position der beteiligten Punkte auswirkt, wenn diese im Datenbestand verbleibt. Hierbei gilt, je größer der Redundanzanteil $r$ ist, desto kleiner ist der Einfluss auf die relative Punktlage. |
Die Wahl eines Schemas zur Hervorhebung der Tabellenzeilen wird unmittelbar auf die dargestellten Tabellen angewendet, vgl. Abbildung 2
Analysediagramme
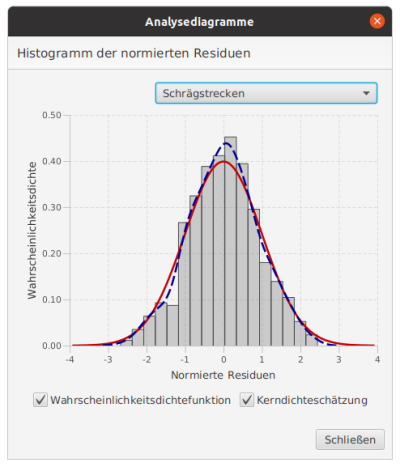
Neben der Bewertung von numerischen Größen in den Datentabellen lassen sich bestimmte Kenngrößen in einer graphischen Analyse häufig schneller erfassen und einordnen. Die Analyse der Residuen zählt zu einen der wichtigsten Methoden, um bspw. systematische Effekte in den Daten zu detektieren. Im einfachsten Fall kann die Analyse der Vorzeichen der Residuen bereits Anhaltspunkte über eine mögliche Asymmetrie bzw. Schiefe (Statistik) liefern, wie bereits Helmert (1924) zeigte.
Die Bewertung kann wahlweise für alle Beobachtungen oder für einen bestimmten Beobachtungstyp erfolgen. Abbildung 3 stellt für die normierten Residuen der terrestrischen Beobachtungen das zugehörige Histogramm (graue Balken) dar. Zur besseren Bewertung kann zusätzlich die Wahrscheinlichkeitsdichtefunktion der Standardnormalverteilung (auch Gauß'sche Glockenkurve) mit eingezeichnet werden (rot). Die Standardnormalverteilung besitzt einen Erwartungswert von Null und eine Varianz von Eins. Aus der erhobenen Stichprobe lässt sich weiterhin die Wahrscheinlichkeitsdichtefunktion mit einer Kerndichteschätzung approximiert. Diese wird optional in blau dargestellt. Zu beachten ist, dass für eine sinnvolle Schätzung ein hinreichend großer Stichprobenumfang vorliegen muss.
