Inhaltsverzeichnis
Einstellungen
Unter dem Menüpunkt Einstellungen im Hauptmenü befinden sich alle projektspezifischen Einstellungen zur Netzausgleichung. Hierzu zählt z.B. das Minimierungsprinzip, die maximale Anzahl an Iterationen oder die Festlegung der Irrtumswahrscheinlichkeit und das Testabstimmungsverfahren für die Hypothesentests.
Ausgleichungseinstellungen
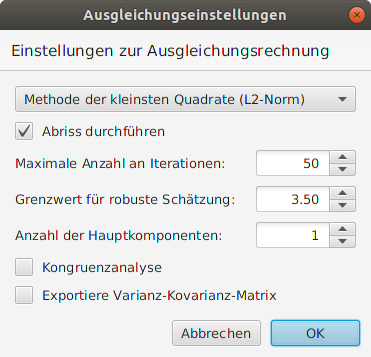
In den Einstellungen zur Ausgleichungsrechnung können globale Parameter für die Berechnung festgelegt werden. Sie finden sich unter Einstellungen → Ausgleichungsrechnung. Im Wesentlichen zählt hierunter das Minimierungsprinzip bzw. die Berechnungsmethode. Die Methode der kleinsten Quadrate ist zwar das Standardverfahren zur Bestimmung von optimalen Parametern aber ungeeignet zum Aufdecken von groben Modellstörungen. Hierfür bieten sich robuste Verfahren zur Lokalisierung an wie bspw. der BIBER-Schätzer.
Weiterhin ermöglicht JAG3D das Durchführen einer Netzplanung, um Konfigurationen und zu erwartende Genauigkeiten für die geplanten Punkte abzuschätzen. Für diese Simulation sind die Netzpunkte und ein Beobachtungsplan vorzugeben. Die numerischen Größen der Beobachtungen bleiben unberücksichtigt, sodass die Beobachtungen mit fiktiven Werten definiert werden können. Die Netzplanung erfolgt üblicherweise iterativ. Konfiguration, Beobachtungsplan und a-priori Unsicherheiten der Beobachtungen werden solange angepasst, bis die gewünschte Netzgenauigkeit und Beobachtungsredundanz erreicht wird.
| Berechnungsmethode | Die Auswertung von erhobenen Messdaten erfolgt wahlweise nach der Methode der kleinsten Quadrate (Default) oder dem robusten Schätzverfahren Bounded Influence By standardizEd Residuals (BIBER-Schätzer). Das robuste Schätzverfahren (L1-Norm) sollte jedoch nur dann angewendet werden, wenn die Methode der kleinsten Quadrate (L2-Norm) aufgrund von sehr groben Modellstörungen unplausible Ergebnisse liefert und eine Lokalisierung dieser nicht möglich ist. Dieser Modus sollte nur zur Bereinigung des Beobachtungsmaterials genutzt werden. In einem finalen Schritt sollten stets Ergebnisse mittels L2-Norm abgeleitet werden. Neben der Auswertung von realen Messdaten kann eine Netzplanung (Simulation) mit fiktiven Beobachtungen durchgeführt werden, um zu erwartende Genauigkeiten abzuschätzen. |
|---|---|
| Varianzfaktor (a-posteriori) berücksichtigen | Für den a-priori Varianzfaktor lässt sich auf der Basis der Beobachtungsresiduen ein Schätzwert angeben, der a-posteriori Varianzfaktor (auch: Varianzfaktor der Gewichtseinheit). Die Zuverlässigkeit der Schätzung hängt von verschiedenen Faktoren ab wie bspw. der Umfang der Stichprobe oder die Streuung der geschätzten Residuen bzgl. der angenommenen Dispersion. Ist eine representative Schätzung des a-posteriori Varianzfaktors nicht möglich, sodass kann auf dessen Berechnung und Berücksichtigung zugunsten des a-priori Varianzfaktors verzichtet werden. |
| Abriss durchführen | Ist diese Option gewählt (Default), so wird vor der eigentlichen Netzausgleichung ein Abriss zur Bestimmung geeigneter Näherungswerte für die Orientierungsunbekannten der Richtungssätze durchgeführt. Ist diese Option nicht ausgewählt, so wird der eingestellte Wert aus den Gruppeneinstellungen verwendet. |
| Konfidenzniveau 1-α | Legt die Sicherheitswahrscheinlichkeit der Konfidenzbereiche einheitlich für alle geschätzten Parameter, d.h. Koordinaten der Punkte und etwaige Zusatzparameter, fest. |
| Maximale Anzahl an Iterationen | Legt die Anzahl der Rechenschritte fest, die zur Bestimmung der Lösung maximal verwendet werden können. Es sind Werte zwischen $0 - 5000$ zulässig, der Defaultwert ist 50. Bei Standardnetzen mit hinreichend guten Näherungswerten reichen meist 5-10 Iterationen, bis der Konvergenzpunkt erreicht wird. Wird häufiger iteriert, so deutet dies meist auf ein Problem in den Daten bzw. Einstellungen hin. |
| Grenzwert für robuste Schätzung | Die in JAG3D integrierte robuste Schätzung basiert auf dem BIBER-Schätzer. Fällt eine Beobachtungsverbesserung in das vorgegebene Intervall, wird diese Beobachtung so behandelt, wie in einer regulären Ausgleichung nach der Methode der kleinsten Quadrate. Liegt sie hingegen außerhalb des Intervalls, wird ihr Einfluss auf die Ausgleichung begrenzt. Der Grenzwert kann zwischen $1,5 - 6,0$ liegen, der Defaultwert ist $3,5$. Die Wahl eines Grenzwertes hat nur Auswirkung auf das Ergebnis, wenn eine robuste Schätzung durchgeführt wird. |
| Anzahl der Hauptkomponenten | Die Hauptkomponentenanalyse ist ein statistisches Werkzeug zur Strukturierung, Charakterisierung und Vereinfachung von umfangreichen Datensätzen in der multivariaten Statistik. Hierzu erfolgt eine spektrale Zerlegung der abgeleiteten Varianz-Kovarianz-Matrix, wobei - entsprechend der vorgegebenen Anzahl - nur die ersten $n$ Eigenwerte und -vektoren bestimmt werden. Die minimale Anzahl beträgt Null, wodurch keine Hauptkomponentenanalyse durchgeführt wird. Die maximale Anzahl der zu schätzenden Hauptkomponenten ergibt sich aus der Dimension der Varianz-Kovarianz-Matrix. Der Defaultwert ist $1$. |
| Kongruenzanalyse | Ist diese Option ausgewählt, prüft JAG3D die Invarianz der epochenübergreifenden Referenzpunkte (Datumspunkte) im Rahmen einer Deformationsanalyse. Hierfür sind die originären Beobachtungen von zwei Messepochen vorzugeben und nach Referenz- bzw. Kontrollepoche zu klassifizieren. Die Kongruenzanalyse setzt zwingend eine freie Netzausgleichung voraus. Diese Option ist standardmäßig nicht ausgewählt. |
| Exportiere Varianz-Kovarianz-Matrix | Ist diese Option ausgewählt, wird die Varianz-Kovarianz-Matrix nach der Ausgleichungsrechnung automatisch ins Projektverzeichnis als ASCII-File geschrieben. Zur Identifizierung der zu den geschätzten Parametern korrespondierenden Zeilen bzw. Spalten wird zusätzlich eine Infodatei erstellt. Diese Option ist standardmäßig nicht ausgewählt. |
Teststatistik
Bei der Durchführung eines Hypothesentests wird die Testgröße der Nullhypothese mit einem kritischen Wert (Quantil) der zugehörigen Verteilung verglichen. Zur Ermittlung des kritischen Wertes ist die Irrtumswahrscheinlichkeit $\alpha$ vorzugeben. Dies ist die Wahrscheinlichkeit, die Nullhypothese abzulehnen obwohl sie richtig ist. In der Statistik wird diese Fehlentscheidung auch als Fehler 1. Art oder Produzentenrisiko bezeichnet.
Entsprechend wird als Konsumentenrisiko bzw. Fehler 2. Art das Annehmen einer nicht zutreffenden Nullhypothese bezeichnet. Somit bezeichnet $\beta$ die Wahrscheinlichkeit, die Alternativhypothese abzulehnen, obwohl sie richtig ist. Durch die Vorgabe von $\alpha$ und $\beta$ liegt der Nichtzentralitätsparameter $\lambda(\alpha,\beta)$ fest, sodass sich die gerade noch aufdeckbare Modellstörung $\nabla(\alpha,\beta)$ dieser Teststatistik bestimmen lässt.
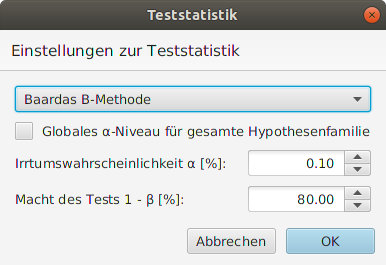
JAG3D stellt zwei in der Geodäsie gebräuchliche Verfahren zur Abstimmung der Irrtumswahrscheinlichkeit zur Verfügung, die sich im Hauptmenü unter Einstellungen → Teststatistik konfigurieren lassen. Dies ist zum einen die auf Baarda zurückgehende B-Methode (oder $\beta$-Methode) und zum anderen die Šidák-Korrektur.
Das gewünschte Abstimmungsverfahren lässt sich über die Auswahlliste einstellen, vgl. Abbildung 2. Ferner ist die Irrtumswahrscheinlichkeit $\alpha$ und die Macht des Tests $1-\beta$ für den Referenztest vorzugeben. Der gewünschten Referenztest kann dabei der Individualtest oder die globale Hypothese sein.
| Abstimmungsverfahren | Das anzuwendende Verfahren zur Testabstimmung (B-Methode (Default), Šidák-Korrektur oder keine Abstimmung) |
|---|---|
| Globales $\alpha$-Niveau für gesamte Hypothesenfamilie | Ist diese Option ausgewählt, so bezieht sich das vorgegebene $\alpha$ und $1 - \beta$ auf die gesamte Hypothesenfamilie (Globaltest). Alle weiteren Teststatistiken werden auf diesen Test abgestimmt. Ist diese Option nicht gewählt, so ist der Individualtest der Referenztest der Abstimmung. Dies ist die Defaulteinstellung. |
| Irrtumswahrscheinlichkeit | Legt das für den Hypothesentest zu nutzende Vertrauensintervall der Nullhypothese fest. Der hinterlegte $\alpha$-Wert wird weiterhin zur Ableitung der Konfidenzbereiche der Koordinaten herangezogen. Zulässige Werte liegen zwischen $0,05-30 \%$. Der Defaultwert ist $\alpha = 0,1 \%$. |
| Macht des Tests | Im Gegensatz zu $\alpha$ wird mit $1 - \beta$ die Wahrscheinlichkeit für das Zutreffen der Alternativhypothese festgelegt. Durch die Vorgabe von $\alpha$ und $\beta$ ist der Nichtzentralitätsparameter $\lambda(\alpha,\beta)$ definiert. Zulässige Werte liegen zwischen $50-99,95 \%$. Der Defaultwert ist $100\% -\beta = 80 \%$. |
Rangdefekt
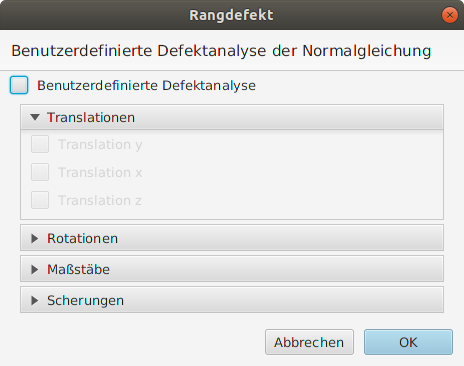
Der Rang der quadratischen Normalgleichungsmatrix beschreibt in der linearen Algebra die Anzahl der linear unabhängigen Gleichungen im Normalgleichungssystem. Ist der Rang einer quadratischen Matrix identisch mit der Anzahl der Zeilen bzw. Spalten, so besitzt diese Matrix vollen Rang. Da terrestrische Messungen nur die relativen geometrischen Beziehungen zwischen den Punkten beschreiben, können diese keinen absoluten Raumbezug definieren. Im Kontext der freien Ausgleichung entstehen daher Normalgleichungssysteme, die keinen vollen Rang besitzen und einen Rangdefekt aufweisen. JAG3D ermittelt anhand des vorgegebenen Beobachtungsmaterials automatisch den Defekt der Normalgleichung und erweitert das Gleichungssystem durch zusätzliche Datumsbedingungen. Diese Datumsbedingungen leiten sich aus einer differenziellen Transformation mit infinitesimalen Drehwinkeln ab.
Anstelle der automatischen Defektanalyse unterstützt JAG3D auch eine nutzerspezifische Vorgabe der zu berücksichtigenden Datumsbedingungen. Entsprechend der gewählten Datumsbedingungen erfolgt die Ränderung des Normalgleichungssystems. Im Rahmen einer Hauptkomponentenanalyse kann hierdurch eine (rechnerische) Versteifung des Systems erreicht werden.
Hinweis: Die vorgegebenen Datumsbedingungen werden von JAG3D nicht validiert und sind daher mit Sorgfalt auszuwählen.
Projektionseinstellungen
Das amtliche Bezugssystem der Bundesrepublik Deutschland ist nach einem Beschluss der Arbeitsgemeinschaft der Vermessungsverwaltungen der Länder der Bundesrepublik Deutschland (AdV) seit Anfang der 1990er Jahre das ETRS89 (European Terrestrial Reference System 1989). Ferner schreibt die AdV für die Verebnung in der Karte die UTM-Projektion mit 6°-Streifenbreite verbindlich vor. Durch diesen Schritt wurden die bisherigen Systeme (bspw. DHDN, S42/83), die mittels Gauß-Krüger-Abbildung verebnet wurden, abgelöst und ein bundesweit einheitliches Bezugssystem geschaffen. Da Projektionen keine (gleichzeitige) längen- und winkeltreue Abbildung der Erdoberfläche ermöglichen, sind die originären Beobachtungen für die Darstellung in der Karte zu reduzieren. Da das amtliche Lage- und Höhennetz unabhängig voneinander definiert sind, ist eine geschlossene Ausgleichung im räumlichen Netz nicht möglich und eine Trennung beider Netzkomponenten ist zwingend.
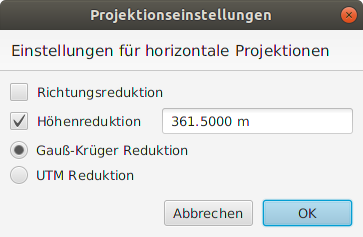
Die UTM-Abbildung ist, ähnlich wie die Gauß-Krüger-Abbildung, eine transversale Merkatorprojektion. Es handelt sich um eine konforme Abbildung, die winkeltreu in kleinsten Teilen ist. Lediglich an den Schnittkreisen des Abbildungszylinders ist die UTM-Projektion längentreu. Der Mittelmeridian eines Streifens wird hingegen um den Maßstab $m_{UTM} = 0,9996$ verkürzt dargestellt und muss bei der sachgerechten Auswertung daher berücksichtigt werden. Weiterhin sind die Strecken in einer Karte auf die Oberfläche des Referenzellipsoids projiziert. Da die tatsächliche Messung der Strecken jedoch an der Erdoberfläche stattfand, ist neben der Projektionsverzerrung auch eine Höhenreduktion zu berücksichtigen, vgl. Abbildung 4.
Im Rahmen einer zweidimensionalen Ausgleichung (2D und 2,5D) mit amtlichem Bezug führt JAG3D die hierfür notwendigen Abbildungsreduktionen optional durch. Der Einstellungsdialog wird über das Hauptmenü Einstellungen → Projektionseinstellungen aufgerufen.
| Richtungsreduktion | Die in Deutschland eingesetzten transversalen Merkatorprojektionen sind winkeltreu in kleinsten Teilen. Bei Netzen mit sehr großer Ausdehnung und weiten Visuren ergibt sich eine projektionsbedingte Verzerrung. Der zur Richtungsreduktion notwendige Projektionsmaßstab ergibt sich in Abhängigkeit der gewählten Projektion zu $m_{UTM} = 0,9996$ bzw. $m_{GK} = 1,0$. |
|---|---|
| Höhenreduktion | Zur Reduktion der gemessenen Horizontalstrecke auf die Oberfläche des Bezugsellipsoids ist eine Höhenreduktion notwendig. Für diese Höhenreduktion ist die mittlere Geländehöhe vorzugeben, vgl. auch Abbildung 4. |
| Merkatorprojektion | Die Verebnung der gemessenen Horizontalstrecke kann wahlweise über die UTM, mit $m_{UTM} = 0,9996$, oder die Gauß-Krüger Streckenreduktion, mit $m_{GK} = 1,0$, erfolgen. |
Hinweis: Eine Reduktion erfolgt nur für die Beobachtungstypen Richtungen und Horizontalstrecken. Räumliche Beobachtungstypen wie bspw. Schrägstrecken oder Zenitwinkel sind unzulässig. Weiterhin müssen die Koordinaten in ungekürzter Form vorliegen, d.h., die Kennziffer bzw. Zonenkennung darf bei GK- bzw. UTM-Koordinaten nicht entfernt werden. Alle aktiven Reduktionen werden in jedem Iterationsschritt zur Laufzeit neu berechnet, um die verbesserte Schätzung der Koordinaten miteinzubeziehen.
Formatierungseigenschaften
JAG3D speichert alle Werte weitgehend im Internationalen Einheitensystem (SI) ab. Für Längen z.B. Höhenunterschiede, Strecken oder Koordinatenkomponenten wird das Meter verwendet. Winkel z.B. Richtungen oder Zenitwinkel werden intern in Radiant gespeichert. Da der direkte Umgang mit diesen SI-Einheiten unüblich ist, formatiert JAG3D die einzelnen Werte vor der Ausgabe, sodass bspw. Winkel in Neugrad (gon) ausgegeben werden. Die gewünschten Formatierungen und Maßeinheiten werden nutzerspezifisch in den Formatierungseigenschaften des Projektes definiert, welches sich unter Hauptmenü Einstellungen → Formatierungseigenschaften befindet. Diese Einstellungen werden auch zur Formatierung im Ausgleichungsreport herangezogen, sofern das Standardtemplate verwendet wird.
Importeinstellungen
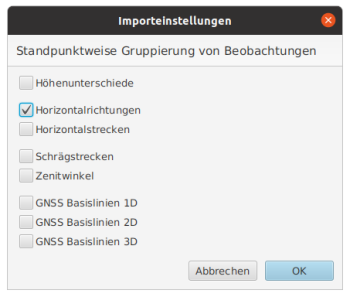
Spaltenbasierte (flache) ASCII-Dateien verfügen allgemein nicht über die nötige Struktur oder zusätzliche Metadaten, die die Art der Daten näher quantifiziert. Beim Import ist daher mindestens der Beobachtungstyp vorzugeben. Über die Einstellungen → Importeinstellungen kann weiterhin spezifiziert werden, ob eine zusätzliche Gruppierung nach Standpunkten erfolgen soll. Im Allgemeinen ist dies bei Richtungsmessungen mit unterschiedlichen Orientierungsunbekannten zwingend nötig. Bei anderen terrestrischen Beobachtungen kann eine Gruppierung sinnvoll sein, wenn eine gesonderte (standpunktweise) Datenanalyse vorgesehen ist.
Ist die Option für einen bestimmten Beobachtungstyp ausgewählt, so markiert ein Wechsel des Standpunktes in der Datei eine neue Beobachtungsgruppe und erzeugt einen zugehörigen separaten Eintrag im Baummenü in JAG3D. Abbildung 5 zeigt die Standardeinstellungen, bei der Richtungen standpunktweise gruppiert werden während des Importvorgangs.
