Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Beobachtungen
JAG3D unterstützt in der Netzausgleichung verschiedene Beobachtungsarten, die innerhalb eines Projektes miteinander kombiniert werden können. Voraussetzung ist, dass die jeweilige Beobachtung zwischen Punkten definiert wird, die diesen Typ unterstützen. Die folgende Tabelle gibt einen Überblick über alle verfügbaren Beobachtungstypen und zwischen welchen Punkten diese in der Ausgleichung berücksichtigt werden können.
| 1D-Punkt | 2D-Punkt | 3D-Punkt | |
|---|---|---|---|
| Nivellement | x | x | |
| Richtung/Azimut | x | x | |
| Horizontalstrecke | x | x | |
| Raumstrecke | x | ||
| Zenitwinkel | x | ||
| GNSS 1D-Basislinie | x | x | |
| GNSS 2D-Basislinie | x | x | |
| GNSS 3D-Basislinie | x | ||
| 1D-Punkt | x | ||
| 2D-Punkt | x | ||
| 3D-Punkt | x | ||
| Lotabweichungen | x |
Das funktionale und stochastische Modell der einzelnen Beobachtungen soll im Folgenden erläutert werden. Beobachtungen sind immer zwischen zwei Punkten definiert, dem Standpunkt $\mathbf{P}_s$ und dem Zielpunkt $\mathbf{P}_z$. Deren Koordinaten seien $\mathbf{P}_s = \begin{pmatrix} x_s & y_s & z_s \end{pmatrix}^{\mathrm{T}}$ und $\mathbf{P}_z = \begin{pmatrix} x_z & y_z & z_z \end{pmatrix}^{\mathrm{T}}$, wenn es sich um Raumpunkte handelt. Liegen die Punkte in einer niederen Dimension vor, so sind die entsprechenden Koordinatenkomponenten zu streichen. Mit $h_s$ und $h_z$ sind die Stand- und Zielpunkthöhen gegeben. Ferner setzt sich das stochastische Modell aus konstanten und entfernungsabhängigen Anteilen zusammen. Die Distanz zur Bestimmung der entfernungsabhängigen Anteile sei mit $d$ bezeichnet.
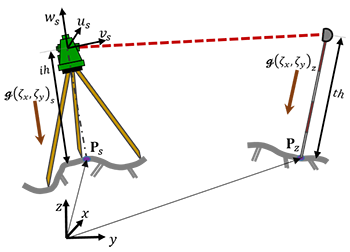
JAG3D unterstützt eine integrierte, hybride 3D-Netzausgleichung für terrestrische Beobachtungen, Nivellements und GNSS-Beobachtungen. Hierbei berücksichtigt die Software eine mögliche Nichtparallelität zwischen den Stehachsen der (Stand-)Punkte infolge von vorhandenen Lotabweichungen (bzw. Stehachsrestneigungen). Abbildung 1 zeigt schematisch den Zusammenhangzwischen dem einheitlich gewählten Datum, dem $x,y,z$-System, und dem jeweils lokalen $u,v,w$-System im Instrumentenstandpunkt.
Werden die Koordinatendifferenzen zwischen zwei Punkten mit
$$ \begin{pmatrix} \Delta x \\ \Delta y \\ \Delta z \\ \end{pmatrix} = \begin{pmatrix} x_z - x_s \\ y_z - y_s \\ z_z - z_s \\ \end{pmatrix} $$
bezeichnet, so ergibt sich die allg. Beobachtungsgleichung
$$ \begin{pmatrix} \Delta u\\ \Delta v\\ \Delta w \end{pmatrix} = \mathbf{R}_s \begin{pmatrix} \Delta x\\ \Delta y\\ \Delta z \end{pmatrix} - \begin{pmatrix} 0\\ 0\\ ih \end{pmatrix} + \mathbf{R}_s\mathbf{R}^{\mathrm{T}}_z \begin{pmatrix} 0\\ 0\\ th \end{pmatrix} $$
worin zur Modellierung der Lotabweichungen (bzw. Stehachsrestneigungen) im Standpunkt die Rotationssequenz $\mathbf{R}_s$ und im Zielpunkt die Rotationssequenz $\mathbf{R}_z$ eingeführt werden. Die Rotationssequenz für jeden Punkt ergibt sich aus einer kombinierten Drehung um die $x$ und $y$-Achse
$$\mathbf{R} = \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos\zeta_x & -\sin\zeta_x \\ 0 & \sin\zeta_x & \cos\zeta_x \\ \end{pmatrix} \begin{pmatrix} \cos\zeta_y & 0 & \sin\zeta_y \\ 0 & 1 & 0 \\ -\sin\zeta_y & 0 & \cos\zeta_y \end{pmatrix}$$
worin $\zeta_x$ und $\zeta_y$ die Drehwinkel zur Beschreibung der Lotabweichungen (bzw. Stehachsrestneigungen) darstellen. Wird die Erde durch eine Kugel approximiert, so lassen sich die Lotabweichungen über die Bogenformel approximieren,
$$\zeta_x = \frac{y - y_0}{R + h_0 - z_0}$$
bzw.
$$\zeta_y = -\frac{x - x_0}{R + h_0 - z_0}$$
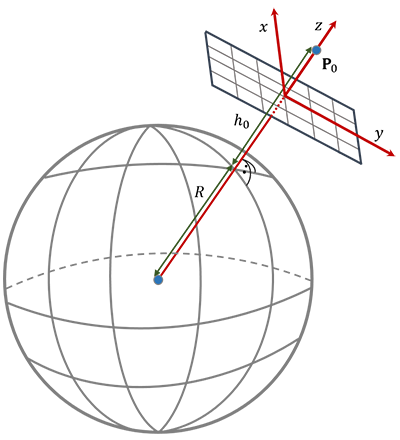
Hierbei beschreibt $\mathbf{P}_0 = \begin{pmatrix} x_0 & y_0 & z_0 \end{pmatrix}^{\mathrm{T}}$ den Fundamentalpunkt (Pivotpunkt), $R$ den Erdradius und $h_0$ die Höhe des Fundamentalpunktes über der Erdkugel, siehe Abbildung 2. Bitte beachte, dass das $x,y,z$-System ein lokales System ist und somit frei definiert werden kann.
Das im Folgenden aufgeführte stochastische Modell wird herangezogen, wenn keine individuellen Genauigkeiten für die einzelnen Beobachtungen vorliegen. In diesem Fall greift der gruppenbasierte Ansatz.
Terrestrische Beobachtungen
Im folgenden werden die terrestrischen Beobachtungsgleichungen, wie sie von JAG3D unterstützt werden, aufgeführt. Neben dem funktionalen Modell wird das stochastische Modell vorgestellt und mögliche Gruppenparameter, die wahlweise als zusätzliche Unbekannte geschätzt werden können, genannt.
Hinweis: Das stochastische Modell setzt sich stets aus einem konstanten und zwei entfernungsabhängigen Anteilen zusammen. Für die entfernungsabhängigen Anteilen muss die Zielweite $d$ gegeben sein. Sollte $d$ nicht explizit vorliegen, berechnet JAG3D die Zielweite näherungsweise aus den Näherungskoordinaten. In Abhängigkeit der Güte der Näherungskoordinaten kann das stochastische Modell daher variieren, sodass die explizite Vorgabe der Zielweite empfohlen wird.
Nivellement
| Funktionales Modell | $\delta h = \frac{1} m \left(w^*_z - w_s\right)$ |
|---|---|
| Stochastisches Modell | $\sigma_{\delta h} = \sqrt{\sigma_a^2 + \sigma_b^2 d + (\sigma_c d)^2}$ |
| Punktdimension | 1D, 3D |
| Zusatzparameter | Maßstab $m$ |
(Bemerkung: $w^*$ bezieht sich auf das lokale System des Zielpunktes)
Richtung/Azimut
| Funktionales Modell | $t = \arctan_2{ \frac{\Delta v} {\Delta u}} - o$ |
|---|---|
| Stochastisches Modell | $\sigma_t = \sqrt{\sigma_a^2 + \left(\frac{\sigma_b} {\sqrt d} \right)^2 + \left(\frac{\sigma_c} d \right)^2 } $ |
| Punktdimension | 2D, 3D |
| Zusatzparameter | Orientierung $o$ |
(Bemerkung: Bei Azimuten entfällt unter Umständen $o$)
Horizontale Strecke
| Funktionales Modell | $s_{2D} = \frac{1} m \left(\sqrt{ \Delta v^2 + \Delta u^2}- a \right)$ |
|---|---|
| Stochastisches Modell | $\sigma_{s_{2D}} = \sqrt{\sigma_a^2 + \sigma_b^2 d + \sigma_c^2 d^2} $ |
| Punktdimension | 2D, 3D |
| Zusatzparameter | Maßstab $m$, Nullpunktabweichung $a$ |
Schrägstrecke
| Funktionales Modell | $s_{3D} = \frac{1} m \left(\sqrt{ \Delta v^2 + \Delta u^2 + \Delta w^2}- a \right)$ |
|---|---|
| Stochastisches Modell | $\sigma_{s_{3D}} = \sqrt{\sigma_a^2 + \sigma_b^2 d + \sigma_c^2 d^2} $ |
| Punktdimension | 3D |
| Zusatzparameter | Maßstab $m$, Nullpunktabweichung $a$ |
Zenitwinkel
| Funktionales Modell | $z = \arctan{ \frac{\sqrt{ \Delta v^2 + \Delta u^2}} {\Delta w}} - k \frac{s_{2D}} {2R} $ |
|---|---|
| Stochastisches Modell | $\sigma_z = \sqrt{\sigma_a^2 + \left(\frac{\sigma_b} {\sqrt d} \right)^2 + \left(\frac{\sigma_c} d \right)^2} $ |
| Punktdimension | 3D |
| Zusatzparameter | Refraktionskoeffizient $k$ |
(Bemerkung: $R = 6371~\rm{km}$ entspricht dem mittleren Erdradius)
GNSS-Basislinien
Im Gegensatz zu den terrestrischen Beobachtungen, bei denen zwischen den Punkten $\mathbf{P}_s$ und $\mathbf{P}_z$ ein einziger Messwert vorliegt, wird die GNSS-Basislinie in Abhängigkeit der Dimension in eine $\mathbf{b}_{1D} = \begin{pmatrix} \delta z \end{pmatrix}^{\mathrm{T}}$, zwei $\mathbf{b}_{2D} = \begin{pmatrix} \delta x & \delta y \end{pmatrix}^{\mathrm{T}}$ oder drei $\mathbf{b}_{3D} = \begin{pmatrix} \delta x & \delta y & \delta z \end{pmatrix}^{\mathrm{T}}$ Vektorkomponenten aufgesplittet. Der Abstand $d$ zur Bildung des entfernungsabhängigen Anteils im stochastischen Modell entspricht hierbei der zugehörigen Basislinenvektorkomponente.
1D-Basislinien
| Funktionales Modell | $\mathbf{b_{1D}} = \delta z = m\mathbf{R} \begin{pmatrix} x_z-x_s \\ y_z-y_s \\ z_z-z_s \end{pmatrix} $ |
|---|---|
| Stochastisches Modell | $\sigma_{\delta z} = \sqrt{\sigma_a^2 + \sigma_b^2 d + \sigma_c^2 d^2}$ |
| Punktdimension | 1D, 3D |
| Zusatzparameter | Maßstab $m$, 2 Drehwinkel in Matrix $\mathbf{R}$ |
(Bemerkung: Bei 1D-Punkten müssen die $x$ und $y$-Koordinaten nur genähert bekannt sein.)
2D-Basislinien
| Funktionales Modell | $\mathbf{b_{2D}} = \begin{pmatrix} \delta x \\ \delta y \end{pmatrix} = m\mathbf{R} \begin{pmatrix} x_z-x_s \\ y_z-y_s \end{pmatrix} $ |
|---|---|
| Stochastisches Modell | $\mathbf{C_b} = \begin{pmatrix} \sigma_{\delta x}^2 & 0 \\ 0 & \sigma_{\delta y}^2 \end{pmatrix}$ worin $\sigma_{\delta} = \sqrt{\sigma_a^2 + \sigma_b^2 d + \sigma_c^2 d^2}$ |
| Punktdimension | 2D, 3D |
| Zusatzparameter | Maßstab $m$, Drehwinkel in Matrix $\mathbf{R}$ |
3D-Basislinien
| Funktionales Modell | $\mathbf{b_{3D}} = \begin{pmatrix} \delta x \\ \delta y \\ \delta z \end{pmatrix} = m\mathbf{R} \begin{pmatrix} x_z-x_s \\ y_z-y_s \\ z_z-z_s \end{pmatrix} $ |
|---|---|
| Stochastisches Modell | $\mathbf{C_b} = \begin{pmatrix} \sigma_{\delta x}^2 & 0 & 0 \\ 0 & \sigma_{\delta y}^2 & 0 \\ 0 & 0 &\sigma_{\delta z}^2 \end{pmatrix}$ worin $\sigma_{\delta} = \sqrt{\sigma_a^2 + \sigma_b^2 d + \sigma_c^2 d^2}$ |
| Punktdimension | 3D |
| Zusatzparameter | Maßstab $m$, 3 Drehwinkel in Matrix $\mathbf{R}$ |
Punktbeobachtungen
Im Rahmen einer weichen Lagerung bzw. dynamischen Ausgleichung werden den stochastischen Anschlußpunkten Unsicherheitsbeiträge zugestanden. Dies erscheint insofern gerechtfertigt, da die Punkte, mit denen der Netzanschluß zu realisieren ist, aus vorherigen Messungen stammen und somit für jeden Punkt neben der Koordinate selbst eine Unsicherheit vorliegt. Die Matrix $\mathbf{I}$ bezeichnet im Folgenden eine Einheitsmatrix.
1D-Punkt
| Funktionales Modell | $\mathbf{P_{1D}} = z = \mathbf{I} z$ |
|---|---|
| Stochastisches Modell | $\mathbf{C_P} = \sigma_z^2$ |
| Punktdimension | 1D |
2D-Punkt
| Funktionales Modell | $\mathbf{P_{2D}} = \begin{pmatrix} x \\ y \end{pmatrix} = \mathbf{I} \begin{pmatrix} x \\ y \end{pmatrix} $ |
|---|---|
| Stochastisches Modell | $\mathbf{C_P} = \begin{pmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_y^2 \end{pmatrix}$ |
| Punktdimension | 2D |
3D-Punkt
| Funktionales Modell | $\mathbf{P_{3D}} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \mathbf{I} \begin{pmatrix} x \\ y \\ z \end{pmatrix} $ |
|---|---|
| Stochastisches Modell | $\mathbf{C_P} = \begin{pmatrix} \sigma_x^2 & 0 & 0 \\ 0 & \sigma_y^2 & 0 \\ 0 & 0 & \sigma_z^2 \end{pmatrix}$ |
| Punktdimension | 3D |
Lotabweichung bzw. Stehachsrestneigung
Bei räumlichen Präzisionsnetzen oder Netzen mit großer Ausdehnung ist die Annahme von parallelen Lotrichtungen für alle (Stand-)Punkte häufig nicht zutreffend. Hier empfiehlt es sich, zusätzliche Parameter zur Kompensation der Lotabweichung bzw. Stehachsrestneigung ins Ausgleichungsmodell zu integrieren. Neben der Berücksichtigung von klassischen terrestrischen Instrumenten wie bspw. Tachymetern können durch die integrierte, hybride 3D-Netzausgleichung auch Messungen von Lasertrackern streng auf der Basis der originären Beobachtungen verarbeitet werden.
| Funktionales Modell | $\mathbf{\zeta} = \begin{pmatrix} \zeta_x \\ \zeta_y \end{pmatrix} = \mathbf{I} \begin{pmatrix} \zeta_x \\ \zeta_y \end{pmatrix} $ |
|---|---|
| Stochastisches Modell | $\mathbf{C_\zeta} = \begin{pmatrix} \sigma_{\zeta_x}^2 & 0 \\ 0 & \sigma_{\zeta_y}^2 \end{pmatrix}$ |
