Inhaltsverzeichnis
Tutorial – Statistisch gesichertes Auffinden von veränderten Punkten mittels Kongruenzanalyse
Die Deformationsanalyse gehört zu den Kernbereichen der Ingenieurgeodäsie. Ziel einer solchen Analyse ist es, statistisch gesicherte Veränderungen an Objekten über einen bestimmten Zeitraum hinweg zu erkennen. Die Datengrundlage resultiert aus der epochalen Erfassung diskreter Punkte, die im Rahmen der Deformationsanalyse auf Kongruenz zu prüfen sind. Klassische Aufgabengebiete können die Überwachung von Rutschhängen oder das Monitoren von Gebäudesetzungen sein.
Um Veränderungen zwischen zwei Messkampagnen am Objekt feststellen zu können, ist ein Zwei-Epochen-Vergleich notwendig. Liegen mehr als zwei Messepochen vor, so ist eine Rückführung auf diesen Fall stets möglich. Einen Vergleich von zwei Messepochen ermöglicht die Ausgleichungssoftware JAG3D auf der Basis der originären Beobachtungen im Rahmen einer gemeinsamen freien Netzausgleichung. Das folgende Beispiel entstammt Baumann (1993).
Die für das Tutorial notwendigen Daten sind als ZIP-Paket zusammengefasst: tutorial_congruenceanalysis.zip.
├───levelling ├───points └───vector
Netzcharakteristik
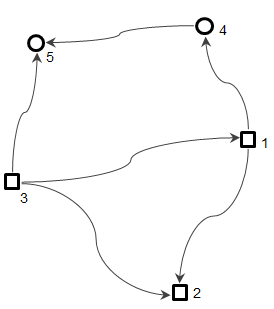
Es handelt sich um das in Abbildung 1 dargestellte einfache Höhennetz, welches aus fünf Punkten besteht und für das Messungen aus zwei Epochen vorliegen. Es liegt ein zweistufiger Netzaufbau vor. Die fünf Netzpunkte unterteilen sich in zwei Objektpunkte (Punkt 4 und 5) und drei Stabil- bzw. Referenzpunkte (Punkt 1, 2 und 3).
In der nachfolgenden Tabelle sind die erhobenen Daten der Referenz- und der Kontrollepoche sowie die zur Bildung des stochastischen Modells heranzuziehenden Nivellementswege aufgelistet. Eine Angabe bezüglich der Instrumentengenauigkeit ist im Baumann (1993) nicht angegeben, sodass ein einheitlicher entfernungsabhängiger Ansatz von 0.0015 m/√km für beide Epochen zu verwenden ist.
| Standpunkt | Zielpunkt | Epoche 0 | Epoche 1 | Nivellementsweg |
|---|---|---|---|---|
| 3 | 1 | 0.247 m | 0.256 m | 600 m |
| 1 | 2 | 5.979 m | 5.980 m | 700 m |
| 3 | 2 | 6.223 m | 6.234 m | 800 m |
| 1 | 4 | 0.379 m | 0.344 m | 300 m |
| 4 | 5 | 0.120 m | 0.115 m | 400 m |
| 3 | 5 | 0.744 m | 0.713 m | 400 m |
Auswertung der Einzelepochen
Bevor die eigentliche Deformationsanalyse durchgeführt werde kann, sollte stets eine separate Auswertung der Einzelepochen erfolgen. Da sich Messabweichungen als Verschiebungen in den Deformationsparametern abbilden würden, dient diese Voranalyse zur Kontrolle der erhobenen Daten und zur Abstimmung des stochastischen Modells. Die Voranalyse erfolgt daher ausschließlich als freie Netzausgleichung, sodass kein äußerer Zwang durch Festpunkte auf das Netz ausgeübt wird. Als Datumspunkte werden die als stabil angenommenen Referenzpunkte 1, 2 und 3 verwendet, während die Punkte 4 und 5 als Neupunkte betrachtet werden.
Hinweis: Bei der Einzelauswertung der Nullepoche wird die Nullhypothese bzgl. einer Modellstörung in der Beobachtung zwischen den Punkten 3 und 1 durch die Teststatistik Tpost verworfen. Aufgrund des geringen Gesamtfreiheitsgrades von lediglich f = 2 ist die Schätzung des a-posteriori Varianzfaktors jedoch nicht zuverlässig, sodass in diesem Fall ausschließlich die Teststatistik Tprio zur Bewertung herangezogen werden sollte.
Da die Objektpunkte in der sich anschließenden Deformationsanalyse getrennt ins Ausgleichungsmodell eingeführt werden, empfiehlt es sich, diese Punkte in jeder Epoche durch ein einheitliches Suffix zu kennzeichnen. In diesem Tutorial werden Objektpunkte der Nullepoche mit _0 und Punkte der Kontrollepoche mit _1 gekennzeichnet. Werden in den Kontrollepochen die ausgeglichenen Koordinaten der Referenzepoche als Näherungswerte vorgegeben, so kann ein direkter Koordinatenvergleich zwischen den ausgewerteten Epochen erste Indizien über die Veränderung des Objektes liefern. Die Veränderungen in den Objektpunkten von über 3 cm deuten auf eine signifikante Änderung dieser Punkte hin. Bei den als stabil angenommenen Punkten ist eine Änderung von über 6 mm im Punkt 3 zu erkennen, die sich gegenüber den Punkten 1 und 2 mit umgekehrten Vorzeichen in den Daten zeigt.
Deformationsanalyse
Das in JAG3D integrierte Modell zur Deformationsanalyse basiert auf der Beobachtungsmethode und entspricht einer gemeinsamen freien Ausgleichung der erhobenen Messelemente beider Epochen. Hierzu werden die als stabil angenommenen Punkte 1, 2 und 3 wiederum als Datumspunkte betrachtet. Die Punkte 4 und 5 werden, wie oben schon geschildert, getrennt nach Epochen mit unterschiedlichen Punktnummern importiert. Weiterhin werden die bereinigten Beobachtungen der Referenz- und Kontrollepoche in getrennte Beobachtungsgruppen importiert und das aus der Einzelauswertung abgestimmte stochastische Modell hinterlegt. Für die Ableitung der Deformationsparameter ist dem Programm bekannt zu machen, zwischen welchen Objektpunkten diese zu erfolgen hat. Die Definition eines (potenziellen) Verschiebungsvektors erfolgt dabei über die epochenweise vergebenen Punktnummern der Objektpunkte.
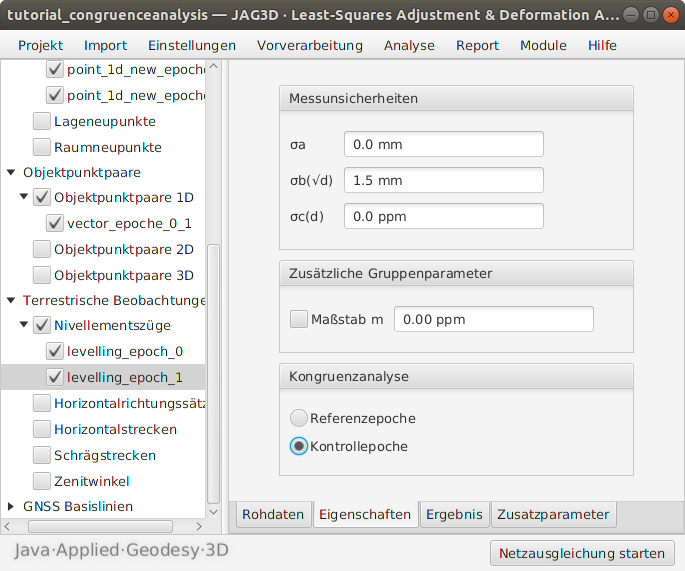
Die Voranalyse lieferte Indizien für Veränderungen in den als stabil angenommenen Punkten. Bevor eine Analyse der Objektpunkte erfolgen kann, ist daher zu untersuchen, ob sich Veränderungen in den Punkten 1, 2 oder/und 3 nachweisen lassen. Hierzu wird das Gauß-Markov-Modell um den möglichen Deformationsanteil des zu prüfenden Referenzpunktes erweitert und auf Signifikanz geprüft. Da das Modell ausschließlich in der Kontrollepoche zu erweitern ist, müssen die Beobachtungsgruppen den einzelnen Epochen zugeordnet werden. In den Gruppeneigenschaften ist daher eine Zuweisung zur Referenzepoche bzw. Kontrollepoche zwingend notwendig, vgl. Abbildung 2.
Weiterhin ist die Option Kongruenzanalyse in den globalen Projekteinstellungen zu setzen und die Ausgleichung zu starten. Bevor die geschätzten Deformationsparameter der Objektpunkte analysiert werden können, ist die Kongruenz der Stabilpunkte sicherzustellen. Die Ergebnisse dieser Kongruenzanalyse finden sich auf dem Reiter Kongruenzanalyse der Punkte der Datumspunktgruppe. Eine gekürzte Darstellung dieses Reiters ist in Abbildung 3 zur sehen.
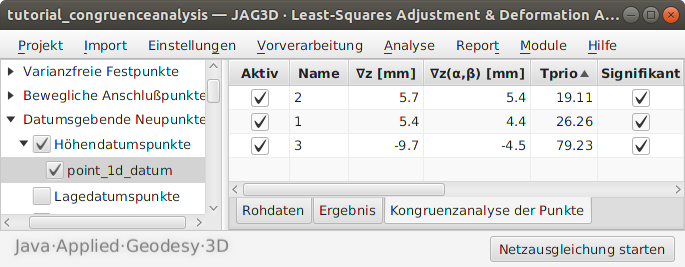
Insbesondere der Punkt 3 weist mit fast 1 cm die größten Deformationsbeträge auf. Auch der Vorzeichenwechsel gegenüber den Punkten 1 und 2, der in der Voranalyse schon auffiel, bestätigt sich. Sowohl die Teststatistik Tprio als auch Tpost ist im Punkt 3 mit Abstand am Größten, sodass analog zur Vorgehensweise des allgemeinen Data-Snoopings zunächst nur dieser Punkt als instabil angenommen wird. Um nicht die fehlerfreien Messungen, an denen der Punkt 3 in der jeweiligen Epoche beteiligt ist, streichen zu müssen, wird der Punkt 3 nicht entfernt sondern als Objektpunkt mit unterschiedlichen Punktnummern in den Epochen im Datenbestand geführt. Der Punkt 3 ist hierzu als Objektpunkt 3_0 und 3_1 in einer Neupunktgruppe zu führen. Die Änderung der Punktnummer ist auch in den jeweiligen Beobachtungsgruppen zu berücksichtigen. Um Fehler zu vermeiden, bietet sich die Suchen und Ersetzen Funktion der Gruppen an. Ferner sollte für den Punkt 3 auch ein Deformationsvektor definiert werden.
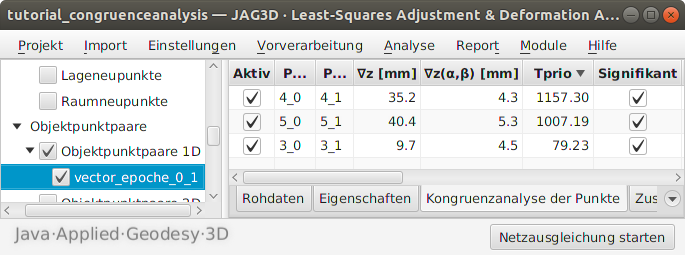
Die erneute Auswertung zeigt, dass in den Punkten 1 und 2 keine signifikant nachweisbaren Änderungen mehr vorliegen, sodass von der Stabilität dieser Punkte auszugehen ist. Die abgeleiteten Deformationsparameter für die Objektpunkte 4, 5 und 3 finden sich auf der Registerkarte Kongruenz der Punkte der Objektpunktpaare und weisen für alle drei Punkte eine deutliche Verschiebung auf. Die Veränderungen von Punkte 4 und 5 liegen bei 3.5-4 cm. Die signifikante Änderung in Punkt 3 beträgt fast 1 cm. Weiterhin ist Anhand der Vorzeichen eine Setzung für alle drei Punkte anzunehmen, vgl. Abbildung 4.
Fazit
In diesem Tutoral wurde anhand eines kleinen Höhennetzes gezeigt, wie mittels JAG3D eine Deformationsanalyse durchgeführt werden kann. Durch statistische Methoden konnte die Instabilität eines Referenzpunktes nachgewiesen werden. In der weiteren Analyse wurde dieser Punkt als Objektpunkt betrachtet. Die nummerisch abgeleiteten Deformationsparameter für die Objektpunkte entsprechen den in Baumann (1993) abgedruckten Ergebnissen bis auf den 1/10 mm und können daher auch als Beleg für die korrekte Berechnung in JAG3D angesehen werden.
