Inhaltsverzeichnis
Tutorial – Softwaregestützte Auswertung klassischer Katasteraufnahmen nach dem Einbinde- und Orthogonalverfahren
Im klassischen Vermessungswesen sind unterschiedliche Verfahren zum Aufmessen von Punkten bekannt. Diese Verfahren zeigen mitunter auch den technischen Fortschritt auf und sind historisch begründet. Das Einbindeverfahren bspw. setzt lediglich ein Streckenmessverfahren – üblicherweise das Messband – voraus. Durch ein Netz aus sogenannten Messungslinien werden die Objektpunkte koordiniert. Beim Orthogonalverfahren werden die Objektpunkte rechtwinklig auf die Messungslinien aufgemessen. Neben der Streckenmessung erfordert dieses Verfahren das Messen von rechten Winkeln bspw. mittels Doppelwinkelprisma. Mit der Einführung von Totalstationen hat sich das Polarverfahren als gängigstes Aufnahmeverfahren etabliert. Dieses Verfahren basiert auf einer kombinierten Strecken und Richtungs- bzw. Winkelmessung. Auch wenn Großteile der Messungen mittels Polarverfahren durchgeführt werden, erfolgen Kontroll- und Ergänzungsmessungen auch heute noch mittels Einbinde- oder Orthogonalverfahren.
Die für das Tutorial notwendigen Daten sind als ZIP-Paket zusammengefasst: tutorial_cadastral-surveying.zip.
├───directions │ ├───dwp │ └───self-evident ├───distance2d └───points
Netzcharakteristik
Moderne Ausgleichungsprogramme bieten häufig keine Möglichkeit, Kleinpunkte direkt zu bestimmen, die auf eine Messungslinie aufgewinkelt wurden. Bedenkt man jedoch, dass es sich auch bei den klassischen Aufnahmeverfahren um Strecken- und (rechte) Winkelmessungen handelt, scheint eine gesonderte Eingabe im Ausgleichungsprogramm unnötig. Im Folgenden soll daher ein Vermessungsriss mit dem Programmsystem JAG3D ausgewertet werden, der lediglich Messungen mit einem Messband und einem Doppelwinkelprisma beinhaltet, vgl. Abbildung 1.
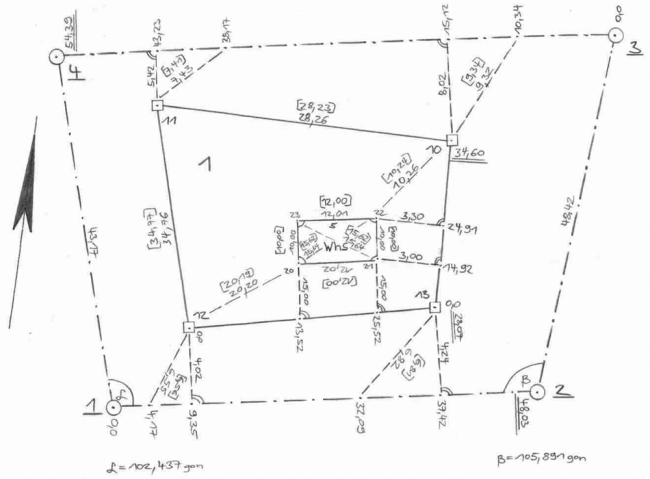
Das Netz schließt am amtlichen Festpunktfeld an. Da hierfür jedoch keine Koordinaten vorliegen, ist ein lokales System zu definieren. Neben den interessierenden Grenz- und Gebäudepunkten sind weitere Hilfs- bzw. Konstruktionspunkte zu definieren. Hierbei handelt es sich bspw. um Lotfußpunkte, die sich durch das Aufnahmeverfahren zwar ergeben aber nur untergeordnet von Interesse sind. Diese Punkte müssen somit eindeutig identifizierbar sein und werden im Rahmen der Ausgleichung mitbestimmt. Es handelt sich hierbei schlicht um Zusatzparameter, die vergleichbar mit den Orientierungsunbekannten von Richtungssätzen beim Polarverfahren sind.
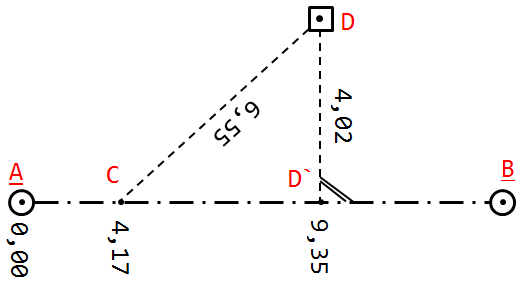
Das Einfluchten eines Punktes in eine Messungslinie bspw. mittels Doppelwinkelprisma kann als eine Winkelmessung interpretiert werden. Ein Punkt C, der auf der Messungslinie zwischen den Punkten A und B liegt, muss demnach einen Winkel von ∡ACB = 200 gon besitzen, vgl. Abbildung 2. Durch die Vorgabe des Abstandes AC oder BC wird der translatorische Defekt, den der Punkt C entlang der Messlinie noch besitzt, behoben. Nach diesem Prinzip sind alle (Hilfs-)Punkte auf den Messungslinien zu parametrieren. Handelt es sich bei D' um einen Lotfußpunkt vom Punkt D, lauten die Winkel ∡AD'D = 100 gon und ∡DD'B = 100 gon, wodurch implizit der Winkel ∡AD'B = 200 gon entsteht. Da JAG3D, wie viele andere Ausgleichungsprogramme auch, keine Eingabe von Winkeln erlaubt, ist jede Winkelmessung in zwei Richtungen zu zerlegen. Die dadurch entstehende Zusatzbeobachtung für die Bezugsrichtung wird durch das Mitschätzen der Orientierungsunbekannten egalisiert. Ordinaten- und Abszissenmaße werden als klassische Streckenbeobachtung in die Ausgleichung eingeführt. Unterschiedliche Maßstäbe können durch entsprechende Streckengruppen berücksichtigt werden.
Netzauswertung
Aus dem Riss in Abbildung 1 wurden alle Messwerte in das JAG3D Standardformat übertragen und Näherungswerte für die Grenz- und Gebäudepunkte als auch für die Konstruktionspunkte ermittelt. Das lokale Datum wird durch die Punkte 1 und 2 definiert, die als Festpunkte importiert werden und somit einen hierarchischen Netzanschluß bilden. Alle übrigen Punkte werden als Neupunkte betrachtet. Nachdem ein Projekt in JAG3D angelegt wurde, erfolgt der Import über das Hauptmenü.
Das stochastische Modell der Streckenmessungen, die mit einem Messband erfolgten, wird im Vergleich zum elektronischen Distanzmesser häufig durch einen Wurzelanteil erweitert. Dieser Ansatz steht für alle Beobachtungsgruppen in JAG3D zur Verfügung. Bei den Richtungen sollte unterschieden werden, ob eine Messung bspw. mit dem Doppelwinkelprisma erfolgt ist (z.B. bei den Lotfußpunkten), oder ob es sich nur um einen augenscheinlichen rechten Winkel handelt (bspw. bei den Gebäudeecken). Die Unsicherheiten der Messungen mittels Doppelwinkelprisma (DWP) können klassisch durch einen additiven und einen streckenabhängigen Ansatz modelliert werden. Sofern auch die nicht gemessenen Winkel in die Auswertung mit einbezogen werden, genügt eine konstante, großzügig abgeschätzte Messunsicherheit. Die nachfolgende Tabelle zeigt ein mögliches stochastisches Modell für die Ausgleichung in JAG3D. Auf dem Reiter Eigenschaften lässt sich für jede Beobachtungsgruppe die gewünschte a-priori Messunsicherheiten definieren.
| Beobachtungen | σa | σb | σc |
|---|---|---|---|
| Messbandstrecken | 7.5 mm | 1 mm/√m | 10 ppm |
| Richtungen (DWP) | 0.02 gon | 0.0 | 5 mm |
| Richtungen (sonstige) | 1.0 gon | 0.0 | 0.0 |
Sind alle Einstellungen getroffen, kann die Berechnung gestartet werden. Abbildung 3 zeigt die nach der Ausgleichung verfügbare Netzskizze. Bedingt durch das lokale Datum, welches durch die Punkte 1 und 2 im südlichen Teil des Netzes definiert wird, werden die Punkte in nördlicher Richtung immer unsicherer. Im Plot kann dies anhand der dargestellten Punktellipsen leicht abgelesen werden.
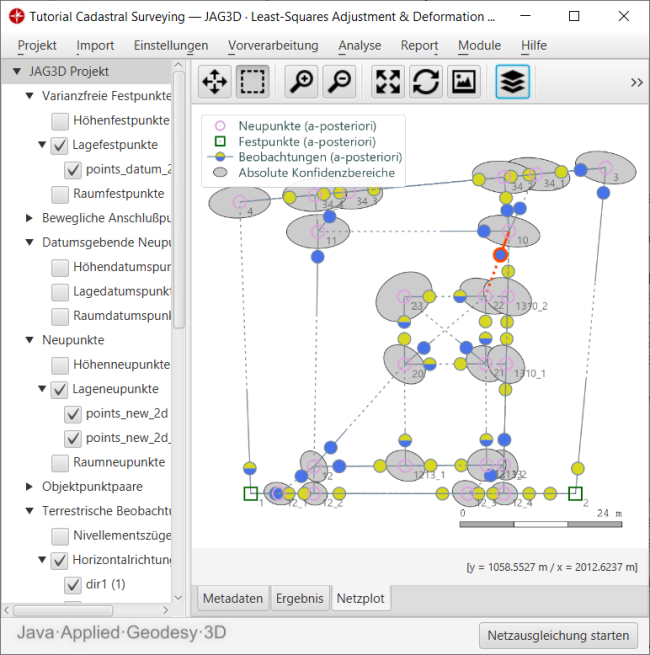
Durch einen Datumswechsel auf die äußeren Punkte 1, 2, 3 und 4 würde dieses Unsicherheitsgefälle aufgelöst werden.
Alternative Vorgehensweise
Einen alternativen Weg hat Edwin Fischer im Forum diskutiert. Unter der Voraussetzung, dass die orthogonalen Winkelmessungen gegenüber den Streckenbeobachtungen mit übergeordneter Genauigkeit erfasst wurden, können die Abszissen- und Ordinatenelemente einer Messungslinie auch als zweidimensionale GNSS Basislinie parametriert werden. Da hierdurch die abgesetzten rechten Winkel implizit durch das funktionale Modell vorgegeben werden, entfällt die explizite Aufschlüsselung durch einzelne Richtungssätze. Insbesondere bei großen Projekten wird hierdurch die Übersicht gewahrt, da neben verbleibenden Spann- bzw. Umringsmaßen nur noch Winkel, die von 100 gon abweichen, zu berücksichtigen sind. Im hier besprochenen Beispiel sind dies lediglich die beiden Winkel α bzw. β. Zusätzlich entfallen die Hilfspunkte, wodurch der Berechnungsprozess beschleunigt wird.
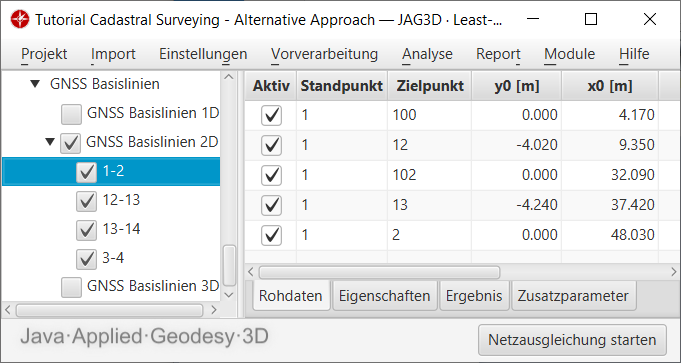
Auf der anderen Seite entfällt jedoch die Möglichkeit, dem gemessenen rechten Winkel eine korrespondierende Messunsicherheit zuzuweisen. Etwaige Unsicherheiten in der Winkelmessung werden somit direkt in die Streckenmessung übertragen und müssen dort berücksichtigt werden. Abbildung 4 zeigt exemplarisch die Abszissen- und Ordinatenwerte der parametrierten Messungslinie zwischen den Punkten 1 und 2 als GNSS Basislinie.
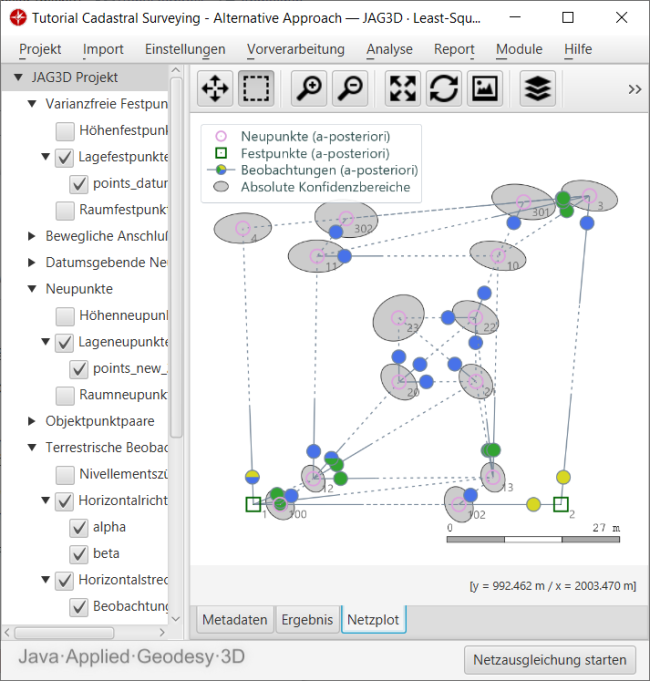
Da jede Messungslinie gegenüber dem globalen Netzdatum eine unterschiedliche Orientierung aufweist, ist ein Mitbestimmen des Rotationswinkels rz als Zusatzparameter zwingend. Dieser ist für jede definierte Gruppe auf dem Reiter Eigenschaften zu aktivieren. Das resultierende Netz ist in Abbildung 5 dargestellt.
Zusammenfassung und Ausblick
Auch klassische Aufnahmen, die mittels Einbindeverfahren oder Orthogonalverfahren realisiert wurden, können mittels der Netzausgleichungssoftware JAG3D sachgerecht ausgewertet werden. Die Notwendigkeit einer speziellen Eingabemaske im Programm ist hierfür nicht nötig, da auch diese Aufnahmemethoden aus Winkel- und Streckenmessungen bestehen und somit alle Voraussetzungen erfüllt sind. Darüber hinaus ist davon auszugehen, dass Messungen mit dem Messband oder dem Doppelwinkelprisma zukünftig weiter an Bedeutung verlieren werden. Die Arbeitsgemeinschaft Anwendung satellitengeodätischer Verfahren in NRW, Dezernat 31 – Katasterwesen, betrachtet bei der Integration der Ausgleichungsrechnung in die Arbeitsabläufe des Liegenschaftskatasters nur noch Messbandmessungen von unter 20 m als zulässig und schlägt vor, auf Messbandmessungen sowie auf die Erhebung orthogonaler Messelemente weitestgehend [zu] verzichten. Ein Aufmass orthogonaler Art, auch von tachymetrischen Aufnahmen abgeleitet, wird nicht mehr zugelassen1).
Insbesondere das höhere Unsicherheitsbudget der Messbandstrecke gegenüber der EDM-Messung ist der Grund für diese Empfehlung. Eine mit Messband bestimmte Strecke kann nur bedingt die polare Aufnahme mittels Tachymeter kontrollieren. Die Zielvorgabe einer durchgreifenden Kontrolle aller Messungen kann somit nicht gewährleistet werden.
